题目内容
【题目】如图所示,菱形![]() 中,
中,![]() ,
,![]() 为
为![]() 中点,
中点,![]() ,
,![]() ,
,![]() ,
,![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .
.

![]() 求证:四边形
求证:四边形![]() 是矩形.
是矩形.
![]() 求
求![]() 的度数.
的度数.
![]() 求菱形
求菱形![]() 的面积.
的面积.
【答案】(1)详见解析;(2)![]() ;(3
;(3![]()
【解析】
(1)先证明四边形四边形![]() 是平行四边形,再证明
是平行四边形,再证明![]() ,根据有一个角是直角的平行四边形为矩形,即可判定四边形AECG是矩形;(2)连接
,根据有一个角是直角的平行四边形为矩形,即可判定四边形AECG是矩形;(2)连接![]() ,易证△ABC是等边三角形,根据等边三角形的性质可得
,易证△ABC是等边三角形,根据等边三角形的性质可得![]() ,同理可得
,同理可得![]() ,即可得
,即可得![]() ,根据两直线平行,同旁内角互补即可求得
,根据两直线平行,同旁内角互补即可求得![]() 的度数;(3)先求得AE的长,再利用菱形
的度数;(3)先求得AE的长,再利用菱形![]() 的面积
的面积![]() 即可求得菱形
即可求得菱形![]() 的面积.
的面积.
![]() 证明:∵四边形
证明:∵四边形![]() 是菱形,
是菱形,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
∵![]() ,
,
∴![]() ,
,
∴四边形![]() 是矩形.
是矩形.
![]() 连接
连接![]() ,如图所示:
,如图所示:
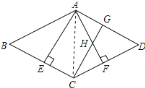
∵![]() 为
为![]() 中点,
中点,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
在等边三角形![]() 中,∵
中,∵![]() ,
,
∴![]() ,
,
同理![]() ,
,
∴![]() ,
,
∵四边形![]() 是矩形,
是矩形,
∴![]() ,
,
∴![]() .
.
![]() ∵
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴菱形![]() 的面积
的面积![]()

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】李老师为了了解学生暑期在家的阅读情况,随机调查了20名学生某一天的阅读小时数,具体情况统计如下:
阅读时间 (小时) | 2 | 2.5 | 3 | 3.5 | 4 |
学生人数(名) | 1 | 2 | 8 | 6 | 3 |
则关于这20名学生阅读小时数的说法正确的是( )
A. 众数是8 B. 中位数是3 C. 平均数是3 D. 方差是0.34