Question

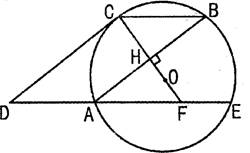
已知：如图，圆Ｏ的半径OC垂直弦AB于点H，连接BC，过点A作弦AE//BC，过点C作CD∥BA交EA延长线于点D，延长CO交AE于点F．

1.求征：CD为圆0的切线

2.若BC =5．AB=8，求OF的长，

 

 

Answer 1

 

1.证明：∵OC⊥AB，CD∥BA，[中国教^&%育*出版网@]

∴∠DCF=∠AHF=90°.

∴CD为⊙O的切线. ……………… 3分

2.解：∵OC⊥AB，AB＝8，

∴AH=BH==4.[中&国#教^育@*出版网]

在Rt△BCH中，∵BH=4，BC=5，

∴CH=3. ………………………………5分[中@#国教育出~&版*网]

∵AE∥BC，∴∠B=∠HAF.

∴△HAF≌△HBC.

∴FH=CH=3，CF=6. …………………………………………………………7分

连接BO，设BO=x，则OC=x，OH=x-3.[中^%&国#教育@出版网]

在Rt△BHO中，由，解得.

∴..…………………………………………………… 9分

解析:（1）证得∠DCF=90°即可证明CD为⊙O的切线；

       （2）在Rt△BHO中，利用勾股定理求得OF的长。