题目内容
在一次知识竞赛中有两种评分规则,一种是从0分开始,答对一题给5分,弃权给2分,答错不给分;另一种是先给40分,然后答对一题给3分,弃权不给分,答错扣1分,某同学在这两种评分规则下都得81分,这次竞赛共有 题.
22
试题分析:设答对a题,未答b题,答错c题,根据题意可得5a+2b=81①,40+3a-c=81②,由①②推出a的取值范围,并确定处a的值,从而推出b、c的值,解决问题.
设答对a题,未答b题,答错c题,可得:
5a+2b=81①,40+3a-c=81②,
由①知,a是奇数,且a≤16;
由②知a≥14,所以a=15,
由此求得b=3,c=4,
故共有:15+3+4=22(题).
答:这张试卷共有22题.
点评:解题的关键是读懂题意,找到等量关系,正确列出方程组,要注意未知数的取值的特征.

练习册系列答案
相关题目
 的正整数解分别为 。
的正整数解分别为 。
 的解是
的解是 则关于x,y的方程组
则关于x,y的方程组 的解是_______________.
的解是_______________. 张制盒身,
张制盒身, 张制盒底,得方程组( )
张制盒底,得方程组( )



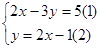 ,把(2)代入(1)得 ( )
,把(2)代入(1)得 ( )