题目内容
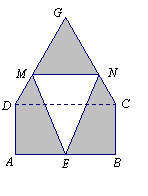
某仓库为了保持库内的湿度和温度,四周墙上均装有如图所示的自动通风设施.该设施的下部ABCD是矩形,其中AB=2米,BC=1米;上部CDG是等边三角形,固定点E为AB的中点.△EMN是由电脑控制其形状变化的三角通风窗(阴影部分均不通风),MN是可以沿设施边框上下滑动且始终保持和AB平行的伸缩横杆.
(1)当MN和AB之间的距离为0.5米时,求此时△EMN的面积;
(2)设MN与AB之间的距离为![]() 米,试将△EMN的面积S(平方米)表示成关于x的函数;
米,试将△EMN的面积S(平方米)表示成关于x的函数;
(3)请你探究△EMN的面积S(平方米)有无最大值,若有,请求出这个最大值;若没有,请说明理由.
 |
解:(1)由题意,当MN和AB之间的距离为0.5米时,MN应位于DC下方,且此时△EMN中MN边上的高为0.5米.
所以,S△EMN= =0.5(平方米).
即△EMN的面积为0.5平方米.
(2)①如图1所示,当MN在矩形区域滑动,
即0<x≤1时,
△EMN的面积S=x;
②如图2所示,当MN在三角形区域滑动,
即1<x<![]() +1 时,
+1 时,
如图,连接EG,交CD于点F,交MN于点H,
∵ E为AB中点,
∴ F为CD中点,GF⊥CD,且FG=![]() .
.
又∵ MN∥CD,
∴ △MNG∽△DCG.
∴![]() ,即 MN=6+2
,即 MN=6+2![]() -2
-2![]() x/3
x/3
故△EMN的面积S=(3+![]() )x-
)x-![]() x²/3
x²/3
综合可得:
S=
![]()
(3)①当MN在矩形区域滑动时,所以有最大值1/2 ;
②当MN在三角形区域滑动时,S=(3+![]() )x-
)x-![]() x²/3 .
x²/3 .
因而,当x= ![]() .+1/2(米)时,S得到最大值,
.+1/2(米)时,S得到最大值,
最大值S=![]() .+1/4(平方米).
.+1/4(平方米).
∵1/2<![]() .+1/4 ,
.+1/4 ,
∴ S有最大值,最大值为![]() .+1/4平方米.
.+1/4平方米.

练习册系列答案
相关题目
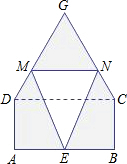 某仓库为了保持库内的湿度和温度,四周墙上均装有如图所示的自动通风设施.该设施的下部ABCD是矩形,其中AB=2米,BC=1米;上部CDG是等边三角形,固定点E为AB的中点.△EMN是由电脑控制其形状变化的三角通风窗(阴影部分均不通风),MN是可以沿设施边框上下滑动且始终保持和AB平行的伸缩横杆.
某仓库为了保持库内的湿度和温度,四周墙上均装有如图所示的自动通风设施.该设施的下部ABCD是矩形,其中AB=2米,BC=1米;上部CDG是等边三角形,固定点E为AB的中点.△EMN是由电脑控制其形状变化的三角通风窗(阴影部分均不通风),MN是可以沿设施边框上下滑动且始终保持和AB平行的伸缩横杆. 下滑动且始终保持和AB平行的伸缩横杆,△EMN是随MN滑动而变化的三角通风窗(阴影部分均不通风).
下滑动且始终保持和AB平行的伸缩横杆,△EMN是随MN滑动而变化的三角通风窗(阴影部分均不通风).
 某仓库为了保持库内的湿度和温度,四周墙上均装有如图所示的自动通风设施.该设施的下部ABCD是矩形,其中AB=2米,BC=1米;上部CDG是等边三角形,固定点E为AB的中点.△EMN是由电脑控制其形状变化的三角通风窗(阴影部分均不通风),MN是可以沿设施边框上下滑动且始终保持和AB平行的伸缩横杆.
某仓库为了保持库内的湿度和温度,四周墙上均装有如图所示的自动通风设施.该设施的下部ABCD是矩形,其中AB=2米,BC=1米;上部CDG是等边三角形,固定点E为AB的中点.△EMN是由电脑控制其形状变化的三角通风窗(阴影部分均不通风),MN是可以沿设施边框上下滑动且始终保持和AB平行的伸缩横杆. 某仓库为了保持库内的湿度和温度,四周墙上均装有如图所示的自动通风设施.该设施的下部ABCD是矩形,其中AB=2米,BC=1米;上部CDG是等边三角形,固定点E为AB的中点.△EMN是由电脑控制其形状变化的三角通风窗(阴影部分均不通风),MN是可以沿设施边框上下滑动且始终保持和AB平行的伸缩横杆.
某仓库为了保持库内的湿度和温度,四周墙上均装有如图所示的自动通风设施.该设施的下部ABCD是矩形,其中AB=2米,BC=1米;上部CDG是等边三角形,固定点E为AB的中点.△EMN是由电脑控制其形状变化的三角通风窗(阴影部分均不通风),MN是可以沿设施边框上下滑动且始终保持和AB平行的伸缩横杆.