题目内容
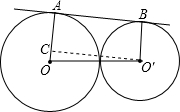
已知⊙O与⊙O′外切于点C,它们的半径分别为R,r,AB为两圆外公切线,切点为A,B,则公切线的长AB等于( )
A.4
| B.
| C.2
| D.2Rr |
如图所示,连接过切点的半径,作O′C⊥OA于C.
在直角三角形OO′C中,OO′=R+r,OC=R-r,
根据勾股定理,得
O′C=
=2
.
故选C.
在直角三角形OO′C中,OO′=R+r,OC=R-r,
根据勾股定理,得
O′C=
| (R+r)2-(R-r)2 |
| Rr |
故选C.


练习册系列答案
相关题目
 直线AE与l相交于点D.
直线AE与l相交于点D.
 ?若成立,给出证明;若不成立,那么AC和AD的长与两圆半径有什么关系?说明理由.
?若成立,给出证明;若不成立,那么AC和AD的长与两圆半径有什么关系?说明理由.


