题目内容
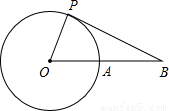
如图,BA与半径为2的⊙O相切于点A,C为⊙O上一点,圆心O在BC上.若∠B=∠C,则AC= .
【答案】分析:连接OA,根据三角形的内角和定理,可求得∠B=∠C=30°,由切线的性质推得∠OAB=90°,再由直角三角形的性质求得AC.
解答: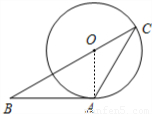 解:如图,连接OA,
解:如图,连接OA,
∵BA与半径为2的⊙O相切于点A,
∴∠OAB=90°,
∵∠B=∠C,
∴AB=AC,
∵OA=OC,
∴∠C=∠OAC,
∴∠B=∠C=30°,
∵OA=2,
∴AB=2 .
.
故答案为:2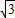 .
.
点评:本题考查了切线的性质,勾股定理、三角形的内角和定理以及直角三角形的性质,是基础知识要熟练掌握.
解答:
 解:如图,连接OA,
解:如图,连接OA,∵BA与半径为2的⊙O相切于点A,
∴∠OAB=90°,
∵∠B=∠C,
∴AB=AC,
∵OA=OC,
∴∠C=∠OAC,
∴∠B=∠C=30°,
∵OA=2,
∴AB=2
 .
.故答案为:2
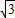 .
.点评:本题考查了切线的性质,勾股定理、三角形的内角和定理以及直角三角形的性质,是基础知识要熟练掌握.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
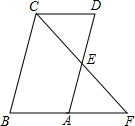
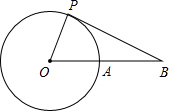
 如图,BA与半径为2的⊙O相切于点A,C为⊙O上一点,圆心O在BC上.若∠B=∠C,则AC=
如图,BA与半径为2的⊙O相切于点A,C为⊙O上一点,圆心O在BC上.若∠B=∠C,则AC=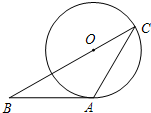 如图,BA与半径为2的⊙O相切于点A,C为⊙O上一点,圆心O在BC上.若∠B=∠C,则AC=________.
如图,BA与半径为2的⊙O相切于点A,C为⊙O上一点,圆心O在BC上.若∠B=∠C,则AC=________.