题目内容
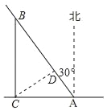
【题目】如图,一船在某灯墙C正东方向10海里处的A点,以25海里/时的速度沿北偏西30°方向航行.
(1)问多长时间后,船距灯塔最近?
(2)求船到达灯塔的正北方向时航行了多少海里?此时,距离灯塔有多远?(结果保留根号)
【答案】(1)0.2小时后,船距灯塔最近;(2)船到达灯塔的正北方向时航行了20海里,此时,距离灯塔有10![]() 海里.
海里.
【解析】
(1)过C作CD⊥AB于D,根据垂线段最近,则CD最小,由三角函数求得CD,再由速度公式求得结论;
(2)根据已知条件利用三角函数即可求得BC,AB的长.
(1)过C作CD⊥AB于D,则CD最小,
由题意知∠BAC=90°﹣30°=60°,
∴AD=![]() AC=5(海里),5÷25=0.2(小时),
AC=5(海里),5÷25=0.2(小时),
故0.2小时后,船距灯塔最近;
(2)在直角△ABC中,∠BAC=60°,AC=10海里,tan∠BAC=![]() ,
,
所以BC=ACtan60°=10![]() 海里,AB=2AC=20海里,
海里,AB=2AC=20海里,
答:船到达灯塔的正北方向时航行了20海里,此时,距离灯塔有10![]() 海里.
海里.

练习册系列答案
相关题目