题目内容
乘法公式的探究及应用:
探究问题:
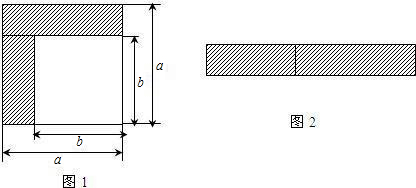
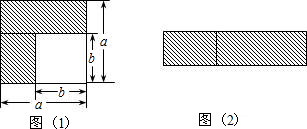
如图1是一张长方形纸条,将其剪成长短两条后刚好能拼成图2,如图所示.
(1)则图1长方形纸条的面积可表示为

(2)拼成的图2中阴影部分面积可表示为

(3)比较两图的阴影部分面积,可以得到乘法公式
结论运用:
(4)应用所得的公式计算:(2x+y)(2x-y)=
m-
)(-
m-
)=
-
m2
-
m2.
拓展运用:
(5)计算:(1-
)(1-
)(1-
)…(1-
)(1-
).
探究问题:
如图1是一张长方形纸条,将其剪成长短两条后刚好能拼成图2,如图所示.
(1)则图1长方形纸条的面积可表示为
(a+b)(a-b)
(a+b)(a-b)
(写成多项式乘法的形式).
(2)拼成的图2中阴影部分面积可表示为
a2-b2
a2-b2
(写成两数平方差的形式).
(3)比较两图的阴影部分面积,可以得到乘法公式
(a+b)(a-b)=a2-b2
(a+b)(a-b)=a2-b2
.结论运用:
(4)应用所得的公式计算:(2x+y)(2x-y)=
4x2-y2
4x2-y2
.(| 2 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 4 |
| 4 |
| 9 |
| 1 |
| 4 |
| 4 |
| 9 |
拓展运用:
(5)计算:(1-
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| 42 |
| 1 |
| 20122 |
| 1 |
| 20132 |
分析:(1)表示出矩形的长和宽,可得出图1长方形纸条的面积;
(2)大正方形的面积减去小正方形的面积,可得阴影部分的面积;
(3)由阴影部分的面积相等,可得出等式;
(4)利用(3)的关系式,即可得出答案;
(5)运用平方差公式将原式拆分,再运算即可.
(2)大正方形的面积减去小正方形的面积,可得阴影部分的面积;
(3)由阴影部分的面积相等,可得出等式;
(4)利用(3)的关系式,即可得出答案;
(5)运用平方差公式将原式拆分,再运算即可.
解答:解:(1)(a+b)(a-b);
(2)a2-b2;
(3)(a+b)(a-b)=a2-b2;
(4)4x2-y2;
-
m2;
(5)原式=(1-
)(1+
)(1-
)(1+
)(1-
)(1+
)…(1-
)(1+
)(1-
)(1+
)
=
×
×
×
×
×
×…×
×
×
×
=
.
(2)a2-b2;
(3)(a+b)(a-b)=a2-b2;
(4)4x2-y2;
| 1 |
| 4 |
| 4 |
| 9 |
(5)原式=(1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2012 |
| 1 |
| 2012 |
| 1 |
| 2013 |
| 1 |
| 2013 |
=
| 1 |
| 2 |
| 3 |
| 2 |
| 2 |
| 3 |
| 4 |
| 3 |
| 3 |
| 4 |
| 5 |
| 4 |
| 2011 |
| 2012 |
| 2013 |
| 2012 |
| 2012 |
| 2013 |
| 2014 |
| 2013 |
=
| 1007 |
| 2013 |
点评:本题考查了平方差公式的几何背景,解答本题的关键是利用阴影部分面积相等得到平方差公式的表达式,注意灵活运用平方差公式.

练习册系列答案
相关题目