题目内容
 (2012•柳州二模)如图,甲船位于灯塔A的东偏南45°,距离灯塔10海里的E处;乙船位于灯塔A的西偏南30°的B处.计划甲船沿正西、乙船沿正东方向驶向位于灯塔A的正南方向的点C处会合.甲船按计划到达,乙船在D点处因遇暗礁被迫停止,乙船经测量发现D点到灯塔的距离与已经航行的距离相同(B、D、C、E在同一直线上).问此时两船共行驶了多少海里?
(2012•柳州二模)如图,甲船位于灯塔A的东偏南45°,距离灯塔10海里的E处;乙船位于灯塔A的西偏南30°的B处.计划甲船沿正西、乙船沿正东方向驶向位于灯塔A的正南方向的点C处会合.甲船按计划到达,乙船在D点处因遇暗礁被迫停止,乙船经测量发现D点到灯塔的距离与已经航行的距离相同(B、D、C、E在同一直线上).问此时两船共行驶了多少海里?分析:根据甲船位于灯塔A的东偏南45°,乙船位于灯塔A的西偏南30°的B处,得出∠E=45°,∠B=30°,再利用锐角三角函数得出AD,BD,以及EC的长,进而得出答案.
解答: 解:∵甲船位于灯塔A的东偏南45°,乙船位于灯塔A的西偏南30°的B处,
解:∵甲船位于灯塔A的东偏南45°,乙船位于灯塔A的西偏南30°的B处,
∴∠E=45°,∠B=30°,
∵AE=10,
∵sin45°=
,
∴AC=5
,
∴CE=5
,
∵tan30°=
,∴BC=5
,
∵BD=AD,∴∠ADC=60°,
∵sin60°=
,
∴BD=AD=
,
BD+CE=5
+
(海里)
答:此时甲、乙两船共行驶了(5
+
)海里.
 解:∵甲船位于灯塔A的东偏南45°,乙船位于灯塔A的西偏南30°的B处,
解:∵甲船位于灯塔A的东偏南45°,乙船位于灯塔A的西偏南30°的B处,∴∠E=45°,∠B=30°,
∵AE=10,
∵sin45°=
| AC |
| AE |
∴AC=5
| 2 |
∴CE=5
| 2 |
∵tan30°=
| AC |
| BC |
| 6 |
∵BD=AD,∴∠ADC=60°,
∵sin60°=
| AC |
| AD |
∴BD=AD=
10
| ||
| 3 |
BD+CE=5
| 2 |
10
| ||
| 3 |
答:此时甲、乙两船共行驶了(5
| 2 |
10
| ||
| 3 |
点评:此题主要考查了锐角三角函数的应用以及方向角问题的应用,根据已知得出BD=AD,∠ADC=60°是解题关键.

练习册系列答案
 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
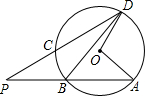 (2012•柳州二模)如图,在⊙O中,弦AB、DC的延长线相交于点P.如果∠AOD=110°,∠BDC=20°,那么∠P=( )
(2012•柳州二模)如图,在⊙O中,弦AB、DC的延长线相交于点P.如果∠AOD=110°,∠BDC=20°,那么∠P=( )