题目内容
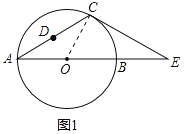
【题目】如图,在△ACE中,CA=CE,∠CAE=30°,⊙O经过点C,且圆的直径AB在线段AE上.
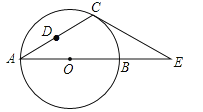
(1)试说明CE是⊙O的切线;
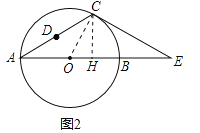
(2)若△ACE中AE边上的高为h,试用含h的代数式表示⊙O的直径AB;
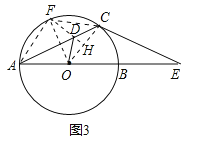
(3)设点D是线段AC上任意一点(不含端点),连接OD,当![]() CD+OD的最小值为6时,求⊙O的直径AB的长.
CD+OD的最小值为6时,求⊙O的直径AB的长.
【答案】(1)证明见试题解析;(2)AB= ![]() ;(3)
;(3)![]() .
.
【解析】试题分析:(1)连接OC,如图1,要证CE是⊙O的切线,只需证∠OCE=90°即可;
(2)过点C作CH⊥AB于H,连接OC,如图2,在Rt△OHC中运用三角函数即可;
(3)作OF平分∠AOC,交⊙O于F,连接AF、CF、DF,如图3,先证四边形AOCF是菱形,由对称性可得DF=DO.过点D作DH⊥OC于H,易得DH=![]() DC,从而有
DC,从而有![]() CD+OD=DH+FD.根据两点之间线段最短可得:当F、D、H三点共线时,DH+FD(即
CD+OD=DH+FD.根据两点之间线段最短可得:当F、D、H三点共线时,DH+FD(即![]() CD+OD)最小,然后在Rt△OHF中运用三角函数即可解决问题.
CD+OD)最小,然后在Rt△OHF中运用三角函数即可解决问题.
试题解析:(1)连接OC,如图1,∵CA=CE,∠CAE=30°,∴∠E=∠CAE=30°,∠COE=2∠A=60°,∴∠OCE=90°,∴CE是⊙O的切线;
(2)过点C作CH⊥AB于H,连接OC,如图2,由题可得CH=h,在Rt△OHC中,CH=OCsin∠COH,∴h=OCsin60°=![]() OC,∴OC=
OC,∴OC=![]() =
= ![]() ,∴AB=2OC=
,∴AB=2OC= ![]() ;
;
(3)作OF平分∠AOC,交⊙O于F,连接AF、CF、DF,如图3,则∠AOF=∠COF=![]() ∠AOC=
∠AOC=![]() (180°﹣60°)=60°,∵OA=OF=OC,∴△AOF、△COF是等边三角形,∴AF=AO=OC=FC,∴四边形AOCF是菱形,∴根据对称性可得DF=DO,过点D作DH⊥OC于H,∵OA=OC,∴∠OCA=∠OAC=30°,∴DH=DCsin∠DCH=DCsin30°=
(180°﹣60°)=60°,∵OA=OF=OC,∴△AOF、△COF是等边三角形,∴AF=AO=OC=FC,∴四边形AOCF是菱形,∴根据对称性可得DF=DO,过点D作DH⊥OC于H,∵OA=OC,∴∠OCA=∠OAC=30°,∴DH=DCsin∠DCH=DCsin30°=![]() DC,∴
DC,∴![]() CD+OD=DH+FD.根据两点之间线段最短可得:当F、D、H三点共线时,DH+FD(即
CD+OD=DH+FD.根据两点之间线段最短可得:当F、D、H三点共线时,DH+FD(即![]() CD+OD)最小,此时FH=OFsin∠FOH=
CD+OD)最小,此时FH=OFsin∠FOH=![]() OF=6,则OF=
OF=6,则OF=![]() ,AB=2OF=
,AB=2OF=![]() ,∴当
,∴当![]() CD+OD的最小值为6时,⊙O的直径AB的长为
CD+OD的最小值为6时,⊙O的直径AB的长为![]() .
.

 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案