题目内容
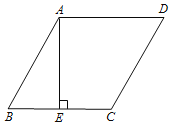
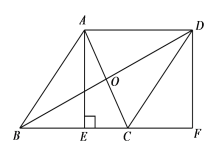
【题目】如图1,已知线段BC=2,点B关于直线AC的对称点是点D,点E为射线CA上一点,且ED=BD,连接DE,BE.
(1)依据题意补全图1,并证明:△BDE为等边三角形;
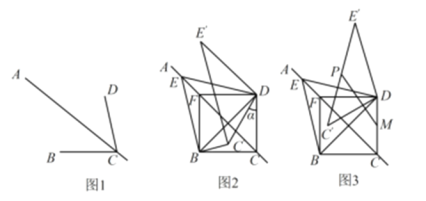
(2)若∠ACB=45°,点C关于直线BD的对称点为点F,连接FD、FB,将△CDE绕点D顺时针旋转![]() 度(0°<
度(0°<![]() <360°)得
<360°)得![]() , 点E的对应点为E’,点C的对应点为点C’.
, 点E的对应点为E’,点C的对应点为点C’.
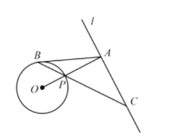
(i)如图2,当![]() 时 ,连接BC’.证明:EF=BC’;
时 ,连接BC’.证明:EF=BC’;
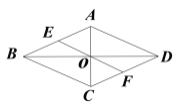
(ii)如图3,点M为DC中点,点P为线段C’E’上任意一点,试探究:在此旋转过程中,线段PM长度的取值范围?(直接写出答案).
【答案】(1)见解析;(2) (i)见解析;(ii)![]() 1≤PM≤2
1≤PM≤2![]() +1.
+1.
【解析】
(1)根据题画图,易证AC是BD的垂直平分线,得到ED=EB=BD,即可证明△BDE为等边三角形;
(2)①易证∠EDB=∠FDC′=60°,∠EDF=BDC′,又DE=DB,DF=DC′于是△EDF≌△DBC′,得出结论;
②当E′C′⊥DC,MP⊥E′C′,D、M、P、C共线时,PM有最小值.当点P与点E′重合,且P、D、M、C共线时,PM有最大值.
(1)补全图形,如图1所示;
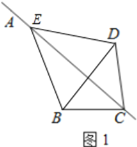
证明:由题意可知:射线CA垂直平分BD,
∴EB=ED,又∵ED=BD,
∴EB=ED=BD,∴△EBD是等边三角形;
(2)(i)证明:如图2:由题意可知∠BCD=90°,BC=DC

又∵点C与点F关于BD对称,∴四边形BCDF为正方形,
∴∠FDC=90°,CD=FD,
∵∠CDC′=α=30°,∴∠FDC′=60°,
由(1)△BDE为等边三角形,
∴∠EDB=∠FDC′=60°,ED=BD,
∴∠EDF=∠BDC′,
又∵△E′DC′是由△EDC旋转得到的,
∴C′D=CD=FD,
∴△EDF≌△DBC′(SAS),
∴EF=BC′;
(ii)线段PM的取值范围是:![]() 1≤PM≤2
1≤PM≤2![]() +1.设射线CA交BD于点O,
+1.设射线CA交BD于点O,
I:如图3(1)

当E′C′⊥DC,MP⊥E′C′,D、M、P、C共线时,PM有最小值.
此时DP=DO=![]() ,DM=1,
,DM=1,
∴PM=DP-DM=![]() 1,
1,
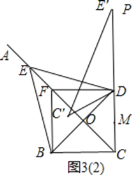
II:如图3(2),
当点P与点E′重合,且P、D、M、C共线时,
PM有最大值.
此时DP=DE′=DE=DB=2![]() ,DM=1,
,DM=1,
∴PM=DP+DM=2![]() +1,
+1,
∴线段PM的取值范围是:![]() 1≤PM≤2
1≤PM≤2![]() +1.
+1.

 阅读快车系列答案
阅读快车系列答案