题目内容
| 如图，从⊙O外一点A作⊙O的切线AB、AC，切点分别为B、C，且⊙O直经BD=6，连结CD、AO。 |
 |
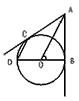| （1）求证：CD∥AO； （2）设CD=x，AO=y，求y与x之间的函数关系式，并写出自变量x的取值范围； |
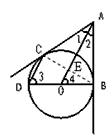
| （1）连接BC交OA于E点 ∵AB、AC是⊙O的切线， ∴AB=AC, ∠1=∠2 ∴AE⊥BC ∴∠OEB=90。 ∵BD是⊙O的直径 ∴∠DCB=90。 ∴∠DCB=∠OEB ； ∴CD∥AO ； （2）∵CD∥AO ∴∠3=∠4 ∵AB是⊙O的切线，DB是直径 ∴∠DCB=∠ABO=90。 ∴△BDC∽△AOB    |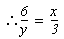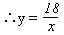
 |
练习册系列答案
相关题目
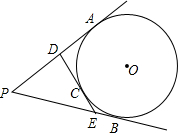如图，从⊙O外一点P引⊙O的两条切线PA、PB，切点分别是A、B，若PA=8cm，C是
如图，从⊙O外一点A作⊙O的切线AB、AC，切点分别为B、C，且⊙O直径BD=6，连接CD、AO．
20、如图，从圆外一点P引圆的切线PA，点A为切点，割线PDB交⊙O于点D、B．已知PA=12，PD=8，则S△ABP：S△DAP=
17、如图，从⊙O外一点A引圆的切线AB，切点为B，连接AO并延长交圆于点C，连接BC．若∠A=26°，则∠ACB的度数为
如图，从⊙O外一点P引⊙O的两条切线PA、PB，切点分别是A、B，若PA=5cm，C是