题目内容
【题目】在平面直角坐标系xOy中,点M的坐标为![]() ,点N的坐标为
,点N的坐标为![]() ,且
,且![]() ,
,![]() ,以MN为边构造菱形,若该菱形的两条对角线分别平行于x轴,y轴,则称该菱形为边的“坐标菱形”.
,以MN为边构造菱形,若该菱形的两条对角线分别平行于x轴,y轴,则称该菱形为边的“坐标菱形”.
(1)已知点A(2,0),B(0,2![]() ),则以AB为边的“坐标菱形”的最小内角为_______;
),则以AB为边的“坐标菱形”的最小内角为_______;
(2)若点C(1,2),点D在直线y=5上,以CD为边的“坐标菱形”为正方形,求直线CD 表达式;
(3)⊙O的半径为![]() ,点P的坐标为(3,m) .若在⊙O上存在一点Q,使得以QP为边的“坐标菱形”为正方形,求m的取值范围.
,点P的坐标为(3,m) .若在⊙O上存在一点Q,使得以QP为边的“坐标菱形”为正方形,求m的取值范围.


【答案】(1)60;(2)![]() 或
或![]() (3)
(3)![]() 或
或![]() .
.
【解析】分析:(1)按要求画出图形,利用锐角三角函数即可求出答案;
(2)根据正方形的对角线分正方形为四个全等的等腰直角三角形,可得出直线CD与直线y=5的夹角是45°.即可找出点D的坐标,利用待定系数法即可求解;
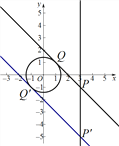
(3)作出比例系数k=1或-1与圆O相切的直线,与直线x=3的交点,即为![]() 的取值范围的界点,即可得出
的取值范围的界点,即可得出![]() 的取值范围.
的取值范围.
详解:(1)如图所示,
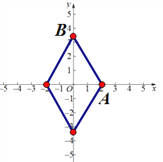
∵![]() ,
,
∴![]() ,
,
∴以AB为边的“坐标菱形”的最小内角为![]() ;
;
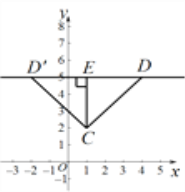
(2)∵以CD为边的“坐标菱形”为正方形,
∴直线CD与直线y=5的夹角是45°.
过点C作CE⊥DE于E.
∴D(4,5)或![]() .
.
∴直线CD的表达式为![]() 或
或![]() .
.
(3)![]() 或
或![]() .
.
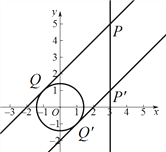

【题目】近日,崂山区教体局对参加2018年崂山区禁毒知识竞赛的2500名初中学生的初试成绩(成绩均为整数)进行一次抽样调查,所得数据如下表:
成绩分组 | 60.5~70.5 | 70.5~80.5 | 80.5~90.5 | 90.5~100.5 |
频数 | 50 | 150 | 200 | 100 |
(1)抽取样本的总人数;
(2)根据表中数据,补全图中频数分布直方图;
(3)若规定初试成绩在90分以上(不包括90分)的学生进入决赛,则全区进入决赛的初中学生约有多少人.

【题目】小明练习跳绳,以1分钟跳165个为目标,并把20次1分钟跳绳的数记录如表(超过165个的部分记为“+”,少于165个的部分记为“-”)
与目标数量的差值 (单位:个) | -12 | -6 | -2 | +5 | +11 |
次数 | 3 | 5 | 4 | 6 | 2 |
(1)小明在这20次跳绳练习中,1分钟最多跳个?
(2)小明在这20次跳绳练习中,1分钟跳绳个数最多的一次比最少的一次多个?
(3)小明在这20次跳绳练习中,累计跳绳多少个?




