题目内容
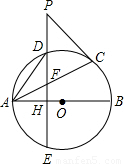 如图,AB、AC分别是⊙O的直径和弦,点D为劣弧AC上一点弦ED⊥AB于H,交AC于点F,延长ED至P,
如图,AB、AC分别是⊙O的直径和弦,点D为劣弧AC上一点弦ED⊥AB于H,交AC于点F,延长ED至P,(1)若PF=PC,求证:PC是⊙O的切线;
(2)当点D在劣弧AC的什么位置时,才能有使AD2=DE•DF,为什么?
【答案】分析:(1)连接OC,根据ED⊥AB,得∠OAC+∠AFH=90°,再由PF=PC,得∠OCA+∠PCA=90°,则PC是⊙O的切线;
(2)连接AE,由题意得△ADF∽△EDA,则弧AD=弧CD,即点D为弧AC的中点.
解答: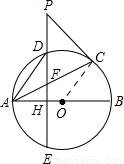 (1)证明:连接OC,
(1)证明:连接OC,
∴OA=OC
∴∠OAC=∠OCA┅┅┅┅┅┅(1分)
∵ED⊥AB
∴∠OAC+∠AFH=90°,
∵PF=PC
∴∠PFC=∠PCF
∴∠OAC+∠PCF=90°
∴∠OCA+∠PCA=90°┅┅┅┅┅┅┅┅(3分)
即OC⊥PC,
故PC是⊙O的切线┅┅┅┅┅┅┅┅(4分)
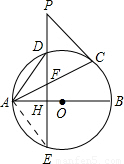 (2)证明:连接AE
(2)证明:连接AE
∵AD2=DE•DF
即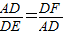
又∵∠ADF=∠EDA
∴△ADF∽△EDA┅┅┅┅┅┅(6分)
∴∠DAF=∠DEA,
∴弧AD=弧CD
即点D为弧AC的中点┅┅┅┅┅┅┅┅┅(7分)
点评:本题考查了切线的判定和性质,相似三角形的判定和性质,是基础知识要熟练掌握.
(2)连接AE,由题意得△ADF∽△EDA,则弧AD=弧CD,即点D为弧AC的中点.
解答:
 (1)证明:连接OC,
(1)证明:连接OC,∴OA=OC
∴∠OAC=∠OCA┅┅┅┅┅┅(1分)
∵ED⊥AB
∴∠OAC+∠AFH=90°,
∵PF=PC
∴∠PFC=∠PCF
∴∠OAC+∠PCF=90°
∴∠OCA+∠PCA=90°┅┅┅┅┅┅┅┅(3分)
即OC⊥PC,
故PC是⊙O的切线┅┅┅┅┅┅┅┅(4分)
 (2)证明:连接AE
(2)证明:连接AE∵AD2=DE•DF
即
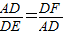
又∵∠ADF=∠EDA
∴△ADF∽△EDA┅┅┅┅┅┅(6分)
∴∠DAF=∠DEA,
∴弧AD=弧CD
即点D为弧AC的中点┅┅┅┅┅┅┅┅┅(7分)
点评:本题考查了切线的判定和性质,相似三角形的判定和性质,是基础知识要熟练掌握.

练习册系列答案
相关题目
 8、已知:如图,AB、AC分别切⊙O于B、C,D是⊙O上一点,∠D=40°,则∠A的度数等于( )
8、已知:如图,AB、AC分别切⊙O于B、C,D是⊙O上一点,∠D=40°,则∠A的度数等于( ) 25、如图,AB、AC分别为⊙O的直径和弦,D为劣弧AC上一点,DE⊥AB于H交⊙O于E,交AC于点F,P为ED延长线上的一点.
25、如图,AB、AC分别为⊙O的直径和弦,D为劣弧AC上一点,DE⊥AB于H交⊙O于E,交AC于点F,P为ED延长线上的一点. 如图,AB、AC分别切⊙O于M、N两点,点D在⊙O上,且∠BDC=60°,则∠A=( )°.
如图,AB、AC分别切⊙O于M、N两点,点D在⊙O上,且∠BDC=60°,则∠A=( )°. 如图,AB、AC分别为⊙O的内接正六边形、内接正方形的一边,BC是圆内接n边形的一边,则n等于( )
如图,AB、AC分别为⊙O的内接正六边形、内接正方形的一边,BC是圆内接n边形的一边,则n等于( )