题目内容
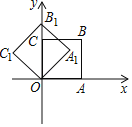
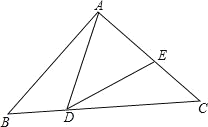
【题目】如图，已知直线y＝kx在第一象限与双曲线y＝
，y＝
分别交于A、B两点，过A、B两点分别作x轴的垂线段，垂足分别为D（1，0）、C（3，0），梯形ABCD的面积为8．求三个函数的解析式．
【答案】双曲线为y＝
，y＝
【解析】
先设A，B的坐标值代入原直线方程，得出a+b的值，再由梯形面积得出关于k的方程，解方程即可求得k，进而求得A、B的坐标，根据待定系数法即可求得k2，k2．
解：已知AD，BC分别垂直于x轴，垂足分别为D（1，0）、C（3，0），故设点A的坐标为（1，a），点B的坐标为（3，b）．
代入y＝kx得a＝k，b＝3k．则a+b＝4k．
又
×（a+b）×（3﹣1）＝8，
∴
＝8，
解得k＝2．
∴直线为y＝2x，
把x＝1代入得y＝2，把x＝3代入得y＝6，
∴A（1，2），B（3，6），
∵双曲线y＝
，y＝
分别过A、B点
∴k1＝1×2＝2．k2＝3×6＝18，
∴双曲线为y＝，y＝．
练习册系列答案
相关题目
