题目内容
 一、请你阅读下列计算过程,再回答所提出的问题:
一、请你阅读下列计算过程,再回答所提出的问题:
题目计算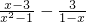
解:原式=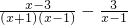 (A)
(A)
=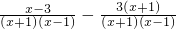 (B)
(B)
=x-3-3(x+1)(C)
=-2x-6(D)
问题:(1)上述计算过程中,从______步开始出现错误;
(2)从(B)到(C)错误的原因是______;
(3)请你正确解答.
二、解方程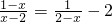
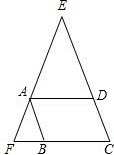
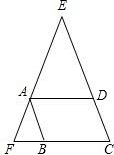
三、如图,?ABCD中,若∠EAD=∠BAF
(1)求证:△CEF是等腰三角形;
(2)△CEF的哪两条边之和恰好等于?ABCD的周长?证明你的结论.
解:一:(1)(A);此处的符号有错,后一式子,分母符号变了,所以分式前面的符号也要变化.改为正号即可.
(2)从(B)到(C)错误的原因是:同分母的分式相加减,分母不变,分子相加减(错误运用分式的运算法则);
(3)正确
解:原式= =
=
二:原方程可变为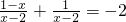 ,
,
即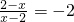 ,
,
得:-2x+4=2-x,
解得x=2,
代入x-2验根,得x=2是增根.
∴原方程无解.
三:(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥DC,
∴∠EAD=∠F,∠FAB=∠E,
∵∠EAD=∠BAF,
∴∠F=∠E,
∴FC=CE,即△CEF是等腰三角形.
(2)FC+CE=?ABCD的周长.
证明:
∵∠EAD=∠F,∠FAB=∠E,∠EAD=∠BAF,
∴∠F=∠BAF,∠E=∠EAD,
∴BF=BA,AD=ED,
∴FC+CE=BC+BF+CD+DE=BC+BA+AD+DC=?ABCD的周长.
分析:(1)根据分式的运算法则就可一步步的算出.但要注意异分母相加减,要先通分,再分母不变分子相加减;
(2)解分式方程即可,但要注意验根;
(3)利用平行线的性质求出AB=BF,AD=DE,∴BF+BC=CD+DE,所以是等腰三角形,由此可知CF,CE的和就是四边形的周长.
点评:一、二题的关键是解分式方程,较简单.主要是第三题要利用平行线的性质找到图中的等角和等边.
(2)从(B)到(C)错误的原因是:同分母的分式相加减,分母不变,分子相加减(错误运用分式的运算法则);
(3)正确
解:原式=
 =
=
二:原方程可变为
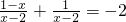 ,
,即
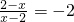 ,
,得:-2x+4=2-x,
解得x=2,
代入x-2验根,得x=2是增根.
∴原方程无解.
三:(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥DC,
∴∠EAD=∠F,∠FAB=∠E,
∵∠EAD=∠BAF,
∴∠F=∠E,
∴FC=CE,即△CEF是等腰三角形.
(2)FC+CE=?ABCD的周长.
证明:
∵∠EAD=∠F,∠FAB=∠E,∠EAD=∠BAF,
∴∠F=∠BAF,∠E=∠EAD,
∴BF=BA,AD=ED,
∴FC+CE=BC+BF+CD+DE=BC+BA+AD+DC=?ABCD的周长.
分析:(1)根据分式的运算法则就可一步步的算出.但要注意异分母相加减,要先通分,再分母不变分子相加减;
(2)解分式方程即可,但要注意验根;
(3)利用平行线的性质求出AB=BF,AD=DE,∴BF+BC=CD+DE,所以是等腰三角形,由此可知CF,CE的和就是四边形的周长.
点评:一、二题的关键是解分式方程,较简单.主要是第三题要利用平行线的性质找到图中的等角和等边.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 一、请你阅读下列计算过程,再回答所提出的问题:
一、请你阅读下列计算过程,再回答所提出的问题: