题目内容
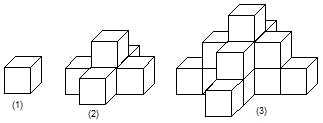
如图所示,是一个水平摆放的小正方体木块,图(1)、(2)、(3)是由这样的小正方体木块叠放而成,按照这样的规律继续叠放下去,至第n个叠放的图形中,最下面一层小正方体木块总数应是

4n-3
4n-3
.
分析:根据前三个图形中最底层的小正方体的个数得到通项公式即可.
解答:解:观察图形知:
第1个图形中最下面一层的小正方体的个数为1=1+4(1-1)个;
第2个图形中最下面一层的小正方体的个数为5=1+4(2-1)个;
第3个图形中最下面一层的小正方体的个数为9=1+4(3-1)个;
…
第n个图形中最下面一层的小正方体的个数为1+4(n-1)=(4n-3)个;
故答案为:4n-3
第1个图形中最下面一层的小正方体的个数为1=1+4(1-1)个;
第2个图形中最下面一层的小正方体的个数为5=1+4(2-1)个;
第3个图形中最下面一层的小正方体的个数为9=1+4(3-1)个;
…
第n个图形中最下面一层的小正方体的个数为1+4(n-1)=(4n-3)个;
故答案为:4n-3
点评:本题考查了图形的变化类问题,解题关键是根据图形的变换总结规律,规律为:最下面一层的小正方体的个数为:4(n-1)+1个.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目