Question

（本题10分）

如图，斜坡AC的坡度（坡比）为1:，AC＝10米．坡顶有一垂直于水平面的旗杆BC，旗杆顶端B点与A点有一条彩带AB相连，AB＝14米．试求旗杆BC的高度．

 

 

Answer 1

【答案】

旗杆的高度为6米

【解析】

Ｅ

试题分析：解：延长BC交AD于E点，则CE⊥AD．

在Rt△AEC中，AC＝10，

由坡比为1: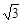可知：tan∠CAE=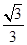，∴∠CAE＝30°．

∴ CE＝AC·sin30°＝10×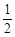＝5，

AE＝AC·cos30°＝10×＝．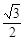

在Rt△ABE中，

BE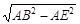＝＝=11．

∵ BE＝BC＋CE，

∴ BC＝BE－CE＝11-5＝6（米）． 

答：旗杆的高度为6米．

考点：解直角三角形

点评：本题难度中等，涉及的知识包括三角函数，坡比，勾股定理。通常把坡面的垂直高度h和水平宽度l的比叫做坡比，即坡角的正切值 (tan a值 a为斜坡与水平面夹角)。学生要能够灵活运用三角函数值来求所需的条件。