题目内容
正方形的对角线的长为2| 2 |
分析:根据正方形对角线互相垂直平分的性质,可以证明△OCD为等腰直角三角形,因为OE⊥CD,所以E为CD的中点,根据斜边中线长为斜边的一半可以求得OE=
CD,∵CD=
=2,故OE=1.
| 1 |
| 2 |
| AC | ||
|
解答: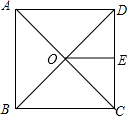 解:图中OE为O到CD边的距离,即OE⊥CD,
解:图中OE为O到CD边的距离,即OE⊥CD,
∵正方形对角线互相垂直平分,
∴OD=OC,OD⊥OC,
即△OCD为等腰直角三角形,
∵OE⊥CD,
∴E为CD的中点,即OE为斜边CD的中线,
∴OE=
CD,
∵在等腰Rt△ADC中,AD=DC,AC=2
,
∴AD=
=2,
即OE=1.
故答案为:1.
 解:图中OE为O到CD边的距离,即OE⊥CD,
解:图中OE为O到CD边的距离,即OE⊥CD,∵正方形对角线互相垂直平分,
∴OD=OC,OD⊥OC,
即△OCD为等腰直角三角形,
∵OE⊥CD,
∴E为CD的中点,即OE为斜边CD的中线,
∴OE=
| 1 |
| 2 |
∵在等腰Rt△ADC中,AD=DC,AC=2
| 2 |
∴AD=
|
即OE=1.
故答案为:1.
点评:本题考查了直角三角形中勾股定理的运用,考查了正方形各边长相等、各内角为直角的性质,考查了正方形对角线互相垂直平分的性质,本题中正确求OE=
CD是解题的关键.
| 1 |
| 2 |

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案
相关题目
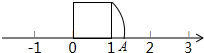

 如图以数轴的单位长度为边作正方形,以数轴上的原点O为圆心,正方形的对角线的长为半径作弧与数轴交于一点A,则点A表示的数为
如图以数轴的单位长度为边作正方形,以数轴上的原点O为圆心,正方形的对角线的长为半径作弧与数轴交于一点A,则点A表示的数为
