Question

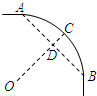（2011•南宁）一条公路弯道处是一段圆弧

AB

，点O是这条弧所在圆的圆心，点C是

AB

的中点，OC与AB相交于点D．已知AB=120m，CD=20m，那么这段弯道的半径为（　　）

• A．200m
• B．200

  3

  m
• C．100m
• D．100

  3

  m

Answer 1

分析：连接OA，由垂径定理求出AD的长，判断出△AOD的形状，在设OA=r，利用勾股定理即可得出r的长．

解答：解：连接OA，
∵C是

AB

的中点，OC与AB相交于点D，
∴AB⊥OC，
∴AD=

1

2

AB=

1

2

×120
=60m，
∴△AOD是直角三角形，
设OA=r，则OD=r-CD=OC-CD=r-20，
在Rt△AOD中，
OA²=AD²+OD²，即r²=60²+（r-20）²，解得r=100m．
故选C．

点评：本题考查的是垂径定理及勾股定理，根据题意作出辅助线，构造出直角三角形是解答此题的关键．