题目内容
用适当的方法解一元二次方程
(1)x2+3x+1=0
(2)x2﹣10x+9=0
(3)(2x﹣1)2=(3x+2)2
(4)(x﹣1)(x+2)=2(x+2)
(1)x2+3x+1=0
(2)x2﹣10x+9=0
(3)(2x﹣1)2=(3x+2)2
(4)(x﹣1)(x+2)=2(x+2)
(1)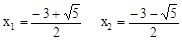 (2)x1=1 x2=9(3)x1=-3 x2=-
(2)x1=1 x2=9(3)x1=-3 x2=- (4)x1=-2 x2=3
(4)x1=-2 x2=3
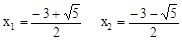 (2)x1=1 x2=9(3)x1=-3 x2=-
(2)x1=1 x2=9(3)x1=-3 x2=- (4)x1=-2 x2=3
(4)x1=-2 x2=3试题分析:
(1)找出a,b,c的值,代入求根公式即可求出解;
(2)方程左边分解因式后,利用两数相乘积为0,两因式中至少有一个为0转化为两个一元一次方程来求解;
(3)利用平方根的定义开方转化为两个一元一次方程来求解;
(4)方程移项后,左边分解因式化为积的形式,利用两数相乘积为0,两因式中至少有一个为0转化为两个一元一次方程来求解.
试题解析:
(1)x2+3x+1=0,
这里a=1,b=3,c=1,
∵b2﹣4ac=9﹣4×1×1=5>0,
∴x=
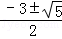 ,
,∴x1=
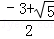 ,x2=
,x2=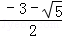 ;
;(2)分解因式得:(x﹣1)(x﹣9)=0,
可得x﹣1=0或x﹣9=0,
解得:x1="1" x2=9;
(3)开方得:2x﹣1=±(3x+2),
即2x﹣1=3x+2或2x﹣1=﹣(3x+2),
∴x1=﹣3,x2=﹣
 ;
;(4)分解因式得:(x+2)(x﹣1﹣2)=0,
可得x+2=0或x﹣3=0,
解得:x1=﹣2,x2=3.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目




 是方程
是方程 的一个根,求方程的另一个根及
的一个根,求方程的另一个根及 的值。
的值。 的一个根是3,求m的值及方程的另一个根.
的一个根是3,求m的值及方程的另一个根. 的两根分别为( )
的两根分别为( ) =-1,=0
=-1,=0 =0
=0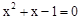 的根为x1、x2,则x1*x2的值为: .
的根为x1、x2,则x1*x2的值为: .



 的两根为
的两根为 ,则
,则 的值是 .
的值是 . ,
, 是一元二次方程
是一元二次方程 的两根,则
的两根,则 的值是( )
的值是( )