题目内容
(2009•梅州一模)大刚与爷爷沿相同的路线同时从山脚出发到达山顶的过程中,各自行进的路程随时间变化的图象如图10所示.请根据图象解答下列问题:
(1)试写出在登山过程中,大刚行进的路程S1(km)与时间t(h)的函数关系式;爷爷行进的路程S2(km)与时间t(h)的函数关系式;(都不要求写出自变量t的取值范围)
(2)当大刚到达山顶时,爷爷行进到出路上某点A处,求点A距山顶的距离;
(3)在(2)的条件下,设爷爷从A处继续登山,大刚到达山顶休息1h后沿原路下山,在距离山顶1.5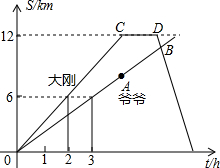 km的B处与爷爷相遇,求大刚下山时的速度.
km的B处与爷爷相遇,求大刚下山时的速度.
(1)试写出在登山过程中,大刚行进的路程S1(km)与时间t(h)的函数关系式;爷爷行进的路程S2(km)与时间t(h)的函数关系式;(都不要求写出自变量t的取值范围)
(2)当大刚到达山顶时,爷爷行进到出路上某点A处,求点A距山顶的距离;
(3)在(2)的条件下,设爷爷从A处继续登山,大刚到达山顶休息1h后沿原路下山,在距离山顶1.5
 km的B处与爷爷相遇,求大刚下山时的速度.
km的B处与爷爷相遇,求大刚下山时的速度.分析:(1)观察图象可得大刚行进的路程S1(km)与时间t(h)的关系与爷爷行进的路程S2(km)与时间t(h)的函数关系式都是正比例函数,然后根据待定系数法求解即可求得答案;
(2)首先根据函数关系式S1=3t求得大刚到达山顶所用时间,然后代入S2=2t,求得爷爷行进的路程,继而可求得点A距山顶的距离;
(3)首先根据题意可求得大刚到达B处用时,利用:速度=
,即可求得大刚下山时的速度.
(2)首先根据函数关系式S1=3t求得大刚到达山顶所用时间,然后代入S2=2t,求得爷爷行进的路程,继而可求得点A距山顶的距离;
(3)首先根据题意可求得大刚到达B处用时,利用:速度=
| 路程 |
| 时间 |
解答:解:(1)设S1=k1t,
∵点(2,6)在S1=k1t图象上,
∴6=2k1,
解得:k1=3,
∴大刚行进的路程S1(km)与时间t(h)的函数关系式为:S1=3t;
设S2=k2t,
∵点(3,6)在S2=k2t图象上,
∴6=3k2,
解得:k2=2,
∴爷爷行进的路程S2(km)与时间t(h)的函数关系式为S2=2t.
(2)∵大刚到达山顶所用时间为:
=4(h),
此时S2=8,12-8=4(km),
即爷爷距山顶的距离为4km.
(3)∵点B与山顶的距离为1.5km,
∴爷爷从山脚到达点B的路程=12-1.5=10.5km,
∴爷爷从山脚到达点B所用的时间为:10.5÷2=
(h),
∴大刚到达B处用时:5.25-5=0.25(h),
∴大刚下山时的速度是:
=6(km/h).
∴大刚下山时的速度是6km/h.
∵点(2,6)在S1=k1t图象上,
∴6=2k1,
解得:k1=3,
∴大刚行进的路程S1(km)与时间t(h)的函数关系式为:S1=3t;
设S2=k2t,
∵点(3,6)在S2=k2t图象上,
∴6=3k2,
解得:k2=2,
∴爷爷行进的路程S2(km)与时间t(h)的函数关系式为S2=2t.
(2)∵大刚到达山顶所用时间为:
| 12 |
| 3 |
此时S2=8,12-8=4(km),
即爷爷距山顶的距离为4km.
(3)∵点B与山顶的距离为1.5km,
∴爷爷从山脚到达点B的路程=12-1.5=10.5km,
∴爷爷从山脚到达点B所用的时间为:10.5÷2=
| 21 |
| 4 |
∴大刚到达B处用时:5.25-5=0.25(h),
∴大刚下山时的速度是:
| 1.5 |
| 0.25 |
∴大刚下山时的速度是6km/h.
点评:此题考查了一次函数的实际应用问题.此题难度适中,解题的关键是根据题意利用待定系数法求得函数解析式,然后利用一次函数解实际问题.

练习册系列答案
 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
 (2009•梅州一模)如图,D、E分别是AB、AC的中点,将△ABC沿线段DE折叠,使点A落在点F处,若S△DEF=4cm2,则梯形BDEC的面积为
(2009•梅州一模)如图,D、E分别是AB、AC的中点,将△ABC沿线段DE折叠,使点A落在点F处,若S△DEF=4cm2,则梯形BDEC的面积为 (2009•梅州一模)如图,AB∥CD,∠BAC与∠DCA的平分线相交于点P.若PE⊥AC于E,且PE=3,则AB与CD之间的距离是
(2009•梅州一模)如图,AB∥CD,∠BAC与∠DCA的平分线相交于点P.若PE⊥AC于E,且PE=3,则AB与CD之间的距离是