题目内容
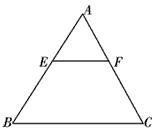
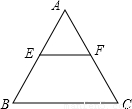
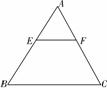
已知：如图，一等边三角形ABC纸片的边长为2a，E是AB边上一动点，（点E与点A、B不重合），过点E作EF∥BC，交AC于点F，设EF=x.
（1）用x的代数式表示△AEF的面积；
（2）将△AEF沿EF折叠，折叠后与四边形BCFE重叠部分的面积为y，求出y关于x的函数关系式，并写出自变量x的取值范围.
 |
(1)解：在等边△ABC中
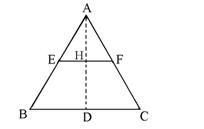作AD⊥BC于D，交EF于H
∴ BD=DC=
又∵ 
tan60°=
∴ AD=
a
∵ EF∥BC
∽
∴ 
=
=
∴ AH=
x
∴ S△AEF=
AH×EF
S△AEF=x2=
x2
(2) 解：①当折叠后△AEF的顶点A落在四边形BCFE内或BC边上时
y=x2 (0＜x≤a ）
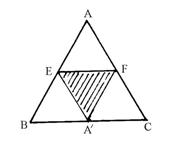
②当折叠后△AEF的顶点A落在四边形BCFE外点A′处时，
A′F交BC于M， A′E交BC于N，连结AA′交EF于H，
交BC于D
∴ =
∴ 
=
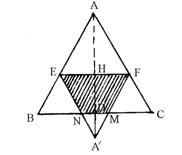又 ∵ AH= A′H
∴ 
=
∴ 
=
∴ 
=
2
=
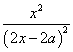
∴ S△A’MN=
∴ S四边形MFEN=x2-
∴ y=-
(a＜x＜2a ）
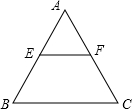已知：如图，一等边三角形ABC纸片的边长为2a，E是AB边上一动点，（点E与点A、B不重合），过点E作EF∥BC，交AC于点F，设EF=x．
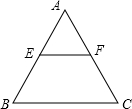已知：如图，一等边三角形ABC纸片的边长为2a，E是AB边上一动点，（点E与点A、B不重合），过点E作EF∥BC，交AC于点F，设EF=x．
