题目内容
(11·西宁)如图10,在⊙O中,AB、AC是互相垂直的两条弦,OD⊥AB于点D,OE⊥AC于点E,且AB=8cm,AC=6cm,那么⊙O的半径OA长为_ ▲ .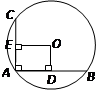

5cm
首先由AB、AC是互相垂直的两条弦,OD⊥AB,OE⊥AC,易证得四边形OEAD是矩形,根据垂径定理,可求得AE与AD的长,然后利用勾股定理即可求得⊙O的半径OA长.
解:连接OA,
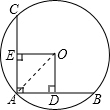
∵OD⊥AB,OE⊥AC,
∴AE=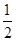 AC=
AC=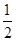 ×6=3(cm),AD=
×6=3(cm),AD=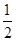 AB=
AB=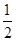 ×8=4(cm),∠OEA=∠ODA=90°,
×8=4(cm),∠OEA=∠ODA=90°,
∵AB、AC是互相垂直的两条弦,
∴∠A=90°,
∴四边形OEAD是矩形,
∴OD=AE=3cm,
在Rt△OAD中,OA=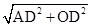 =5cm.
=5cm.
故答案为:5cm.
解:连接OA,

∵OD⊥AB,OE⊥AC,
∴AE=
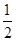 AC=
AC=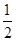 ×6=3(cm),AD=
×6=3(cm),AD=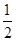 AB=
AB=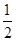 ×8=4(cm),∠OEA=∠ODA=90°,
×8=4(cm),∠OEA=∠ODA=90°,∵AB、AC是互相垂直的两条弦,
∴∠A=90°,
∴四边形OEAD是矩形,
∴OD=AE=3cm,
在Rt△OAD中,OA=
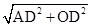 =5cm.
=5cm.故答案为:5cm.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
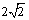 的圆经过一个半径为4的圆的圆心,则图中阴影部分的面积为 。
的圆经过一个半径为4的圆的圆心,则图中阴影部分的面积为 。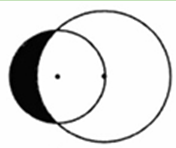
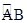 ,点O是这条弧所在圆的圆心,点C是
,点O是这条弧所在圆的圆心,点C是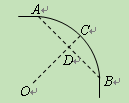
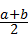 与
与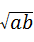 的大小关系是
的大小关系是 ●探究证明
●探究证明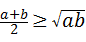 .
.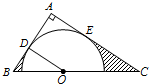
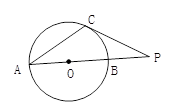 ∠BAC=30°,过点C作⊙O的切线交AB的延长线于点
∠BAC=30°,过点C作⊙O的切线交AB的延长线于点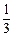 ,求DE的长.
,求DE的长.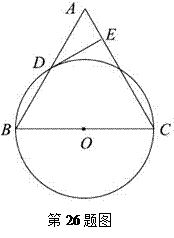
 ,∠COD=60°.
,∠COD=60°.