题目内容
 体育用品商场为了推销某一运动服,先做了市场调查,得数据如表:
体育用品商场为了推销某一运动服,先做了市场调查,得数据如表:| 卖出价格x(元/件) | 50 | 51 | 52 | 53 | … |
| 销售量p(件) | 500 | 490 | 480 | 470 | … |
(2)如果这种运动服的买入价为每件40元,试求销售利润y(元)与卖出价格x(元/件)的函数关系式(销售利润=销售收入-成本);并求当卖出价为多少时,能获得最大利润?获得最大利润是多少?
分析:(1)根据表格依次描点、连线,根据图象判断p与x的函数关系式;
(2)根据(1)的表格求出p与x的函数关系式,根据利润=(卖出价格每件x元-买入价为每件40元)×销售量p,列出函数式,根据二次函数的性质求最大利润.
(2)根据(1)的表格求出p与x的函数关系式,根据利润=(卖出价格每件x元-买入价为每件40元)×销售量p,列出函数式,根据二次函数的性质求最大利润.
解答:解:(1)描点、连线如图所示,可判断p与x满足一次函数关系式;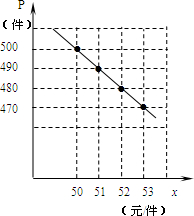
设p与x的函数关系式为p=kx+b,将(50,500),(51,490)代入,
得
,解得
,
所以,p=-10x+1000,
(2)销售利润为y元,
则y=(x-40)p=(x-40)(-10x+1000)=-10x2+1400x-40000=-10(x-70)2+9000,
∵-10<0,抛物线开口向下,当x=70时,y有最大值为9000,
∴当卖出价为每件70元时,能获得最大利润,最大利润为9000元.

设p与x的函数关系式为p=kx+b,将(50,500),(51,490)代入,
得
|
|
所以,p=-10x+1000,
(2)销售利润为y元,
则y=(x-40)p=(x-40)(-10x+1000)=-10x2+1400x-40000=-10(x-70)2+9000,
∵-10<0,抛物线开口向下,当x=70时,y有最大值为9000,
∴当卖出价为每件70元时,能获得最大利润,最大利润为9000元.
点评:本题考查了二次函数与一次函数的应用.关键是根据图象判断一次函数,根据利润的计算方法得出二次函数关系式,利用二次函数的性质解题.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
东海体育用品商场为了推销某一运动服,先做了市场调查,得到数据如下表:
(1)以x作为点的横坐标,p作为纵坐标,把表中的数据,在图中的直角坐标系中描出相应的点,观察连接各点所得的图形,判断p与x的函数关系式;
(2)如果这种运动服的买入价为每件40元,试求销售利润y(元)与卖出价格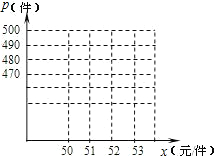 x(元/件)的函数关系式(销售利润=销售收入-买入支出);
x(元/件)的函数关系式(销售利润=销售收入-买入支出);
(3)在(2)的条件下,当卖出价为多少时,能获得最大利润?
| 卖出价格x(元/件) | 50 | 51 | 52 | 53 | … |
| 销售量p(件) | 500 | 490 | 480 | 470 | … |
(2)如果这种运动服的买入价为每件40元,试求销售利润y(元)与卖出价格
 x(元/件)的函数关系式(销售利润=销售收入-买入支出);
x(元/件)的函数关系式(销售利润=销售收入-买入支出);(3)在(2)的条件下,当卖出价为多少时,能获得最大利润?
州东海体育用品商场为了推销某一运动服,先做了市场调查,得到数据如下表:
| 卖出价格x(元/件) | 50 | 51 | 52 | 53 | …… |
| 销售量p(件) | 500 | 490 | 480 | 470 | …… |
(1) 以x作为点的横坐标,p作为纵坐标,把表中的数据,在图中的直角坐标系中描出相应的点,观察连结各点所得的图形,判断p与x的函数关系式;
(2) 如果这种运动服的买入件为每件40元,试求销售利润y(元)与卖出价格x(元/件)的函数关系式(销售利润=销售收入-买入支出);
(3) 在(2)的条件下,当卖出价为多少时,能获得最大利润?
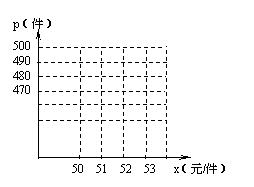
东海体育用品商场为了推销某一运动服,先做了市场调查,得到数据如下表:
(1)以x作为点的横坐标,p作为纵坐标,把表中的数据,在图中的直角坐标系中描出相应的点,观察连接各点所得的图形,判断p与x的函数关系式;
(2)如果这种运动服的买入价为每件40元,试求销售利润y(元)与卖出价格x(元/件)的函数关系式(销售利润=销售收入-买入支出);
(3)在(2)的条件下,当卖出价为多少时,能获得最大利润?
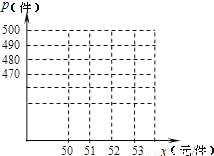
| 卖出价格x(元/件) | 50 | 51 | 52 | 53 | … |
| 销售量p(件) | 500 | 490 | 480 | 470 | … |
(2)如果这种运动服的买入价为每件40元,试求销售利润y(元)与卖出价格x(元/件)的函数关系式(销售利润=销售收入-买入支出);
(3)在(2)的条件下,当卖出价为多少时,能获得最大利润?

东海体育用品商场为了推销某一运动服,先做了市场调查,得到数据如下表:
(1)以x作为点的横坐标,p作为纵坐标,把表中的数据,在图中的直角坐标系中描出相应的点,观察连接各点所得的图形,判断p与x的函数关系式;
(2)如果这种运动服的买入价为每件40元,试求销售利润y(元)与卖出价格x(元/件)的函数关系式(销售利润=销售收入-买入支出);
(3)在(2)的条件下,当卖出价为多少时,能获得最大利润?
| 卖出价格x(元/件) | 50 | 51 | 52 | 53 | … |
| 销售量p(件) | 500 | 490 | 480 | 470 | … |
(2)如果这种运动服的买入价为每件40元,试求销售利润y(元)与卖出价格x(元/件)的函数关系式(销售利润=销售收入-买入支出);
(3)在(2)的条件下,当卖出价为多少时,能获得最大利润?
