题目内容
已知等腰梯形的上底为2,下底为4,腰长为2,则该等腰梯形的面积为
3
| 3 |
3
.| 3 |
分析:分别过A,D作AE⊥BC,DF⊥BC,则四边形ADFE是矩形,根据已知可求得CF的长,再根据勾股定理求得DF的长,从而利用梯形的面积公式求解即可.
解答:解:如图,AD=2,BC=4,CD=2,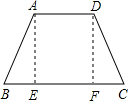
分别过A,D作AE⊥BC,DF⊥BC,则四边形ADFE是矩形,
∴AD=EF,BE=CF=
(BC-AD)=1.
在直角△CDF中,DF=
=
∴S梯形ABCD=
(2+4)
=3
,
故答案为:3
.

分别过A,D作AE⊥BC,DF⊥BC,则四边形ADFE是矩形,
∴AD=EF,BE=CF=
| 1 |
| 2 |
在直角△CDF中,DF=
| CD2-CF2 |
| 3 |
∴S梯形ABCD=
| 1 |
| 2 |
| 3 |
| 3 |
故答案为:3
| 3 |
点评:本题考查梯形面积的求法,难度不大,关键是利用勾股定理求出梯形的高.

练习册系列答案
相关题目