Question

一个三角形两边中点的连线叫做这个三角形的中位线．只要顺次连结三角形三条中位线，则可将原三角形分割为四个全等的小三角形（如图（1））；把三条边分成三等份，再按照图（2）将分点连起来，可以看作将整个三角形分成9个全等的小三角形；把三条边分成四等份，…，按照这种方式分下去，第n个图形中应该得到个全等的小三角形．

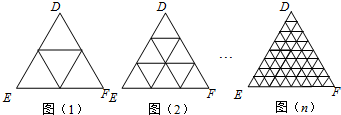
1. A.
   
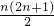
2. B.
   
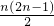
3. C.
   
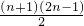
4. D.
   （n+1）²

Answer 1

D
分析：第一图形中三角形的个数为4，第二个图形中三角形的个数为9，这两个数均为完全平方数，那么就可得到第n个图形中全等的三角形个数．
解答：由图（1）可知：顺次连接各中点所得全等的小三角形为1+3=（1+1）²；
图（2）中顺次连接各中点所得全等的小三角形为1+3+5=（2+1）²；
同理如果把三条边分成3等分可得到1+3+5+7=（3+1）²个全等的小三角形，按照这种方式分下去，第n个图形中应该得到（n+1）²个全等的小三角形．
故选：D．
点评：本题考查了三角形中位线定理，用加法表示出全等三角形的个数，进而找到相应规律是解决本题的关键．