��Ŀ����
����Ŀ���ڱ߲���ȵ�ƽ���ı���ֽƬ����ȥһ�����Σ�����һ���ı��Σ���Ϊ��һ�β����������µ��ı���ֽƬ���ټ�ȥһ�����Σ���ʣ��һ���ı��Σ���Ϊ�ڶ��β��������������ƣ�����n�β������µ��ı��������Σ����ԭƽ���ı���Ϊn�����Σ���ͼ��ABCD�У���AB=1��BC=2����ABCDΪ1�����Σ�
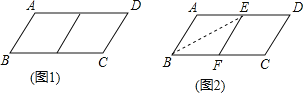
��1�����������
���ڱ߳��ֱ�Ϊ2��3��ƽ���ı����� �����Σ�
��С��Ϊ�˼�ȥһ�����Σ����������²�������ͼ����ABCD��BE�۵�����E��AD�ϣ���ʹ��A����BC���ϵĵ�F���õ��ı���ABFE����֤���ı���ABFE�����Σ�
��2��������̽������㣺
����֪ABCD���ڱ߳��ֱ�Ϊ1��a��a��1��������3�����Σ��뻭��ABCD���ü��ߵ�ʾ��ͼ������ͼ���·�д��a��ֵ��
����֪ABCD���ڱ߳��ֱ�Ϊa��b��a��b��������a=6b+r��b=5r����д��ABCD�Ǽ������Σ�
���𰸡���1����2����֤����������(2)��![]() ��
��![]() ��
��![]() ��4��10.
��4��10.
��������
��1���ٸ����ڱ߳��ֱ�Ϊ2��3��ƽ���ı��ξ������β��������ɵó���ʣ�ı��������Σ����ɵó��𰸣�
�ڸ���ƽ���ı��ε����ʵó�AE��BF�������ó�AE=BF�����ɵó��𰸣�
��2��������3�����εĶ��壬���ɵó��𰸣�
�ڸ���a=6b+r��b=5r����r��ʾ�����߳�����������ͼ�εó�ABCD�Ǽ������Σ�
��1���������ڱ߳��ֱ�Ϊ2��3��ƽ���ı��ξ������β�������ʣ�ı����DZ߳�Ϊ1�����Σ�
���ڱ߳��ֱ�Ϊ2��3��ƽ���ı�����2�����Σ�
�����۵�֪����ABE=��FBE��AB=BF��
���ı���ABCD��ƽ���ı��Σ�
��AE��BF��
���AEB=��FBE��
���AEB=��ABE��
��AE=AB��
��AE=BF��
���ı���ABFE��ƽ���ı��Σ�
���ı���ABFE�����Σ�
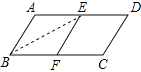
��2������ͼ��ʾ��
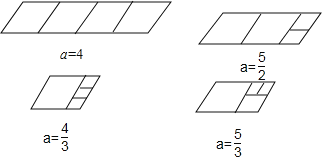 ��
��
�ڴ�10�����Σ�
��a=6b+r��b=5r��
��a=6��5r+r=31r��
��ͼ��ʾ��
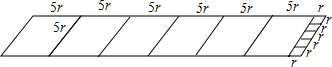
��ABCD��10������

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�����Ŀ��ij�̳�������һ������������ת��ת�̣����涨���˿���10Ԫ���Ͼ��ܻ��һ��ת��ת�̵Ļ��ᣬ��ת��ֹͣʱ��ָ��������һ����Ϳ��Ի����Ӧ�Ľ�Ʒ.�±��ǻ�����е�һ�����ڽ�Ʒ��Ǧ�ʡ������ͳ�����ݣ�
ת��ת�̵Ĵ��� | 100 | 150 | 200 | 500 | 800 | 1000 |
���ڡ�Ǧ�ʡ��Ĵ��� | 68 | 111 | 136 | 345 | 564 | 701 |
���ڡ�Ǧ�ʡ��ijɹ��� |
��1��.���㲢��ɱ���ȷ��0.01����
��2��.����ƣ���![]() �ܴ�ʱ�����ڡ�Ǧ�ʡ������Ƶ�ʽ���ӽ�______����ȷ��0.1��.
�ܴ�ʱ�����ڡ�Ǧ�ʡ������Ƶ�ʽ���ӽ�______����ȷ��0.1��.
��3��.������ȥת����ת��һ�Σ�����Ǧ�ʵijɹ���Լ��______.