题目内容
如图,已知二次函数y=ax2+bx+3的图象与x轴相交于点A、C,与y轴相交于点B,A(-| 9 | 4 |
(1)求C点坐标、∠ABC的度数及二次函数y=ax2+bx+3的关系式;
(2)在线段AC上是否存在点M(m,0).使得以线段BM为直径的圆与边BC交于P点(与点B不
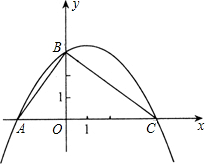 同),且以点P、C、O为顶点的三角形是等腰三角形?若存在,求出m的值;若不存在,请说明理由.
同),且以点P、C、O为顶点的三角形是等腰三角形?若存在,求出m的值;若不存在,请说明理由.
分析:(1)由二次函数y=ax2+bx+3的解析式,首先求出B点坐标,然后由△AOB∽△BOC,根据相似三角形的对应边成比例,求出OC的长度,得出C点坐标;根据相似三角形的对应角相等得出∠OAB=∠OBC,从而得出∠ABC=90°;由y=ax2+bx+3图象经过点A(-
,0),C(4,0),运用待定系数法即可求出此二次函数的关系式;
(2)如果以点P、C、O为顶点的三角形是等腰三角形,那么分三种情况讨论:①CP=CO;②PC=PO;③OC=OP.针对每一种情况,都应首先判断M点是否在线段AC上,然后根据相似三角形的对应边成比例求出m的值.
| 9 |
| 4 |
(2)如果以点P、C、O为顶点的三角形是等腰三角形,那么分三种情况讨论:①CP=CO;②PC=PO;③OC=OP.针对每一种情况,都应首先判断M点是否在线段AC上,然后根据相似三角形的对应边成比例求出m的值.
解答:解:(1)由题意,得B(0,3),
∵△AOB∽△BOC,
∴∠OAB=∠OBC,
∴
=
,
∴
=
,
∴OC=4,∴C(4,0);
∴∠OAB+∠OBA=90°,
∴∠OBC+∠OBA=90°,
∴∠ABC=90°;
∵y=ax2+bx+3图象经过点A(-
,0),C(4,0),
∴
,
∴y=-
x2+
x+3;
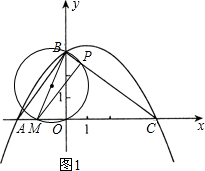 (2)①如图1,当CP=CO时,点P在BM为直径的圆上,
(2)①如图1,当CP=CO时,点P在BM为直径的圆上,
因为BM为圆的直径,
∴∠BPM=90°,
∴PM∥AB,
∴△CPM∽△CBA,
∴CM:CA=CP:CB,
CM:6.25=4:5,
∴CM=5,
 ∴m=4-5=-1;
∴m=4-5=-1;
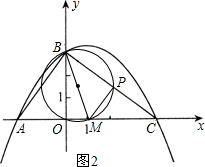
②如图2,当PC=PO时,点P在OC垂直平分线上,
得PC=
BC=2.5,
由△CPM∽△CBA,得CM=
,
∴m=4-
=
;
③当OC=OP时,M点不在线段AC上.
综上所述,m的值为
或-1.
∵△AOB∽△BOC,
∴∠OAB=∠OBC,
∴
| OA |
| OB |
| OB |
| OC |
∴
| 2.25 |
| 3 |
| 3 |
| OC |
∴OC=4,∴C(4,0);
∴∠OAB+∠OBA=90°,
∴∠OBC+∠OBA=90°,
∴∠ABC=90°;
∵y=ax2+bx+3图象经过点A(-
| 9 |
| 4 |
∴
|
∴y=-
| 1 |
| 3 |
| 7 |
| 12 |
 (2)①如图1,当CP=CO时,点P在BM为直径的圆上,
(2)①如图1,当CP=CO时,点P在BM为直径的圆上,因为BM为圆的直径,
∴∠BPM=90°,
∴PM∥AB,
∴△CPM∽△CBA,
∴CM:CA=CP:CB,
CM:6.25=4:5,
∴CM=5,
 ∴m=4-5=-1;
∴m=4-5=-1;②如图2,当PC=PO时,点P在OC垂直平分线上,
得PC=
| 1 |
| 2 |
由△CPM∽△CBA,得CM=
| 25 |
| 8 |
∴m=4-
| 25 |
| 8 |
| 7 |
| 8 |
③当OC=OP时,M点不在线段AC上.
综上所述,m的值为
| 7 |
| 8 |
点评:本题着重考查了待定系数法求二次函数解析式,相似三角形的性质,探究等腰三角形的构成情况等重要知识点,综合性强,能力要求高.考查学生分类讨论,数形结合的数学思想方法.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
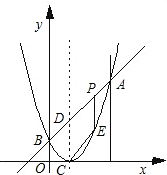
 三角形与△BOF相似?若存在,请求出P点的坐标;若不存在,请说明理由.
三角形与△BOF相似?若存在,请求出P点的坐标;若不存在,请说明理由.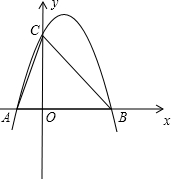
 如图,已知二次函数图象的顶点坐标为C(1,0),直线y=x+b与该二次函数的图象交于A、B两点,其中点A的坐标为(3,4),点B在y轴上.点P为线段AB上的一个动点(点P与A、B不重合),过点P作x轴的垂线与该二次函数的图象交于点E.
如图,已知二次函数图象的顶点坐标为C(1,0),直线y=x+b与该二次函数的图象交于A、B两点,其中点A的坐标为(3,4),点B在y轴上.点P为线段AB上的一个动点(点P与A、B不重合),过点P作x轴的垂线与该二次函数的图象交于点E.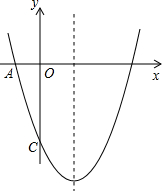 如图,已知二次函数y=ax2-4x+c的图象与坐标轴交于点A(-1,0)和点C(0,-5).
如图,已知二次函数y=ax2-4x+c的图象与坐标轴交于点A(-1,0)和点C(0,-5).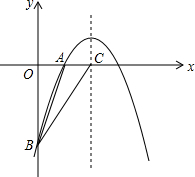 (2012•衡水一模)如图,已知二次函数
(2012•衡水一模)如图,已知二次函数