题目内容
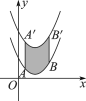
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 的对称轴为
的对称轴为![]() .
.
![]() 求
求![]() 的值及抛物线
的值及抛物线![]() 与
与![]() 轴的交点坐标;
轴的交点坐标;
![]() 若抛物线
若抛物线![]() 与
与![]() 轴有交点,且交点都在点
轴有交点,且交点都在点![]() ,
,![]() 之间,求
之间,求![]() 的取值范围.
的取值范围.
【答案】(1) a=-1;坐标为![]() ,
,![]() ;(2)
;(2)![]() .
.
【解析】
(1)利用抛物线的对称轴方程得到x=-![]() =-1,解方程求出a即可得到抛物线的解析式为y=-x2-2x;然后解方程-x2-2x=0可得到抛物线与x轴的交点坐标;
=-1,解方程求出a即可得到抛物线的解析式为y=-x2-2x;然后解方程-x2-2x=0可得到抛物线与x轴的交点坐标;
(2)抛物线y=-x2-2x+m由抛物线y=-x2-2x上下平移|m|和单位得到,利用函数图象可得到当x=1时,y<0,即-1-2+m<0;当x=-1时,y≥0,即-1+2+m≥0,然后解两个不等式求出它们的公共部分可得到m的范围.
![]() 根据题意得
根据题意得![]() ,解得
,解得![]() ,
,
所以抛物线的解析式为![]() ,
,
当![]() 时,
时,![]() ,解得
,解得![]() ,
,![]() ,
,
所以抛物线与![]() 轴的交点坐标为
轴的交点坐标为![]() ,
,![]() ;
;
![]() 抛物线抛物线
抛物线抛物线![]() 由抛物线
由抛物线![]() 上下平移
上下平移![]() 和单位得到,而抛物线的对称轴为直线
和单位得到,而抛物线的对称轴为直线![]() ,
,
∵抛物线![]() 与
与![]() 轴的交点都在点
轴的交点都在点![]() ,
,![]() 之间,
之间,
∴当![]() 时,
时,![]() ,即
,即![]() ,解得
,解得![]() ;
;
当![]() 时,
时,![]() ,即
,即![]() ,解得
,解得![]() ,
,
∴![]() 的取值范围为
的取值范围为![]() .
.

练习册系列答案
相关题目
【题目】某校八年级甲.乙两班分别选5名同学参加“学雷锋读书活动”演讲比赛,其预赛成绩如图:
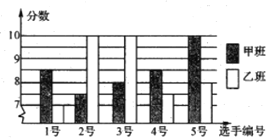
(1)根据上图求出下表所缺数据:
平均数 | 中位数 | 众数 | 方差 | |
甲班 | 8.5 | 8.5 | ||
乙班 | 8 | 1.6 |
(2)根据上表中的平均数、中位数和方差你认为哪班的成绩较好?并说明你的理由.