题目内容
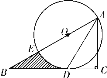
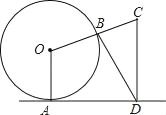
【题目】如图,直线l与⊙O相切于点A,作半径OB并延长至点C,使得BC=OB,作CD⊥直线l于点D,连接BD得∠CBD=75°,则∠OCD=_____度.
【答案】70.
【解析】
过点B作BE⊥AD于点D,连接AB,利用BC=OB、CD⊥AD及AD为⊙O切线可证得△BAD为等腰三角形,此时可利用∠BAD=∠BDA找到∠C与∠O的关系,从而可以求出∠C的度数.
解:过点B作BE⊥AD于点D,连接AB,
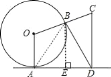
∵直线l与⊙O相切于点A,
∴OA⊥AD,
∵CD⊥AD,
∴OA∥BE∥CD,
∴∠O+∠C=180°,
∵OB=BC,
∴AE=ED,
∴BA=BD,
∴∠BAE=∠BDE,
∵直线l与⊙O相切于点A,
∴∠O=2∠BAE,
∴∠O=2∠BDE,
∵∠CBD=75°,CD⊥AD,
∴∠BDC=105°﹣∠C,∠BDE=90°﹣(105°﹣∠C)=∠C﹣15°,
∴∠O=2(∠C﹣15°)=2∠C﹣30°,
∴2∠C﹣30°+∠C=180°,解得∠C=70°.
故答案为:70.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
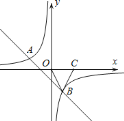
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于
的图象交于![]() ,
,![]() 两点.
两点.
![]() Ⅰ
Ⅰ![]() 试确定上述反比例函数和一次函数的表达式;
试确定上述反比例函数和一次函数的表达式;
![]() Ⅱ
Ⅱ![]() 连OB,在x轴上取点C,使
连OB,在x轴上取点C,使![]() ,并求
,并求![]() 的面积;
的面积;
![]() Ⅲ
Ⅲ![]() 直接写出一次函数值大于反比例函数值的自变量x的取值范围.
直接写出一次函数值大于反比例函数值的自变量x的取值范围.