��Ŀ����
��ͼ����ֱ������ϵ�У�����ABCD�ı�AD��y���������ϣ���A��C������ֱ�Ϊ��0��1������2��4������P�ӵ�A��������A?B?C��ÿ��1����λ���ٶ��˶�������Cֹͣ����Q��x���ϣ�������Ϊ��P�ĺᡢ������֮�ͣ�������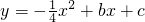 ����A��C���㣮����P��x��Ĵ��ߣ�����
����A��C���㣮����P��x��Ĵ��ߣ�����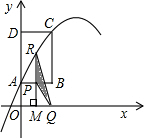 ΪM�����������ڵ�R�����P���˶�ʱ��Ϊt���룩����PQR�����ΪS��ƽ����λ����
ΪM�����������ڵ�R�����P���˶�ʱ��Ϊt���룩����PQR�����ΪS��ƽ����λ����
��1���������߶�Ӧ�ĺ�����ϵʽ��
��2���ֱ���t=1��t=4ʱ����Q�����ꣻ
��3����0��t��5ʱ����S��t֮��ĺ�����ϵʽ����ֱ��д��S�����ֵ��
�ο���ʽ��������y=ax2+bx+c�Ķ�������Ϊ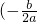 ��
��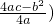 ��
��
�⣺��1���������߾�����A��0��1����C��2��4����
�� ��
��
��� ��
��
�������߶�Ӧ�ĺ�����ϵʽΪ��y=- x2+2x+1��
x2+2x+1��
��2����t=1ʱ��P������Ϊ��1��1����
��Q��������2��0����
��t=4ʱ��P������Ϊ��2��3����
��Q��������5��0����
��3����0��t��5��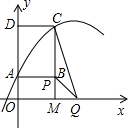
��0��t��2ʱ��S= ��-
��- t2+2t+1-1����1��
t2+2t+1-1����1��
S=- t2+t=-
t2+t=- ��t-4��2+2��
��t-4��2+2��
��t=4����0��t��2��
�൱t=2ʱ����ͼ��ʾ����S�����ֵΪ1.5��
��2��t��5ʱ��S= ��5-t����2+t-2+1-2����
��5-t����2+t-2+1-2����
S=- t2+3t-
t2+3t- =-
=- ��t-3��2+2��
��t-3��2+2��
��˵�t=3ʱ��S�����ֵΪ2��
����������S�����ֵΪ2��
��������1�����������߹�A��C���㣬��˿ɸ���A��C�������ô���ϵ������������ߵĽ���ʽ��
��2����t=1ʱ��P��AB�ϣ�AP=1���P�������Ϊ��1��1����Q������Ϊ��2��0����
��t=4ʱ����ʱP��BC�ϣ���BP=4-AB=2��P�������Ϊ��2��3����Q�������Ϊ��5��0��
��3������Ҫ����������������ۣ�
�ٵ�P��AB��ʱ������0��t��2ʱ��AP=t��OQ=t+OA=t+1��MQ=t+1-t=1����P�ĺ����꼴t���������ߵĽ���ʽ�м������R���������ֵ��RM�ij������������PR�ij����ɴ˿ɸ���S��RPQ= RP•MQ=
RP•MQ= PR�����S��t�ĺ�����ϵʽ�������ɸ��ݺ������������S�����ֵ��
PR�����S��t�ĺ�����ϵʽ�������ɸ��ݺ������������S�����ֵ��
�ڵ�P��BC��ʱ������2��t��5ʱ��BP=t-AB=t-2��PM=t-AB+OA=t-1������ʱR��C�غϣ����RM=4�����RP=5-t����
QM=OQ-AB=2+��t-2+1��-2=t-1��Ȼ����ݢٵķ����������S�����ֵ��
�������������ؿ����˴���ϵ��������κ�������ʽ�Լ����κ�����Ӧ�ã��ڣ�3������Ҫ����P��IJ�ͬλ�ý��з������ۣ���Ҫ©�⣮
��
 ��
�����
 ��
���������߶�Ӧ�ĺ�����ϵʽΪ��y=-
 x2+2x+1��
x2+2x+1����2����t=1ʱ��P������Ϊ��1��1����
��Q��������2��0����
��t=4ʱ��P������Ϊ��2��3����
��Q��������5��0����
��3����0��t��5��

��0��t��2ʱ��S=
 ��-
��- t2+2t+1-1����1��
t2+2t+1-1����1��S=-
 t2+t=-
t2+t=- ��t-4��2+2��
��t-4��2+2����t=4����0��t��2��
�൱t=2ʱ����ͼ��ʾ����S�����ֵΪ1.5��
��2��t��5ʱ��S=
 ��5-t����2+t-2+1-2����
��5-t����2+t-2+1-2����S=-
 t2+3t-
t2+3t- =-
=- ��t-3��2+2��
��t-3��2+2����˵�t=3ʱ��S�����ֵΪ2��
����������S�����ֵΪ2��
��������1�����������߹�A��C���㣬��˿ɸ���A��C�������ô���ϵ������������ߵĽ���ʽ��
��2����t=1ʱ��P��AB�ϣ�AP=1���P�������Ϊ��1��1����Q������Ϊ��2��0����
��t=4ʱ����ʱP��BC�ϣ���BP=4-AB=2��P�������Ϊ��2��3����Q�������Ϊ��5��0��
��3������Ҫ����������������ۣ�
�ٵ�P��AB��ʱ������0��t��2ʱ��AP=t��OQ=t+OA=t+1��MQ=t+1-t=1����P�ĺ����꼴t���������ߵĽ���ʽ�м������R���������ֵ��RM�ij������������PR�ij����ɴ˿ɸ���S��RPQ=
 RP•MQ=
RP•MQ= PR�����S��t�ĺ�����ϵʽ�������ɸ��ݺ������������S�����ֵ��
PR�����S��t�ĺ�����ϵʽ�������ɸ��ݺ������������S�����ֵ���ڵ�P��BC��ʱ������2��t��5ʱ��BP=t-AB=t-2��PM=t-AB+OA=t-1������ʱR��C�غϣ����RM=4�����RP=5-t����
QM=OQ-AB=2+��t-2+1��-2=t-1��Ȼ����ݢٵķ����������S�����ֵ��
�������������ؿ����˴���ϵ��������κ�������ʽ�Լ����κ�����Ӧ�ã��ڣ�3������Ҫ����P��IJ�ͬλ�ý��з������ۣ���Ҫ©�⣮

��ϰ��ϵ�д�
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
�����Ŀ

 ��ͼ����ֱ������ϵ�У���P������Ϊ��3��4������OP��ԭ��O��ʱ����ת90��õ��߶�OP�䣮
��ͼ����ֱ������ϵ�У���P������Ϊ��3��4������OP��ԭ��O��ʱ����ת90��õ��߶�OP�䣮

 ��2����������ABC������λ��ͼ�Ρ�A1B1C1����A2B2C2��ͬʱ������������������
��2����������ABC������λ��ͼ�Ρ�A1B1C1����A2B2C2��ͬʱ������������������