题目内容
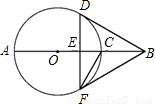
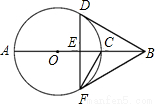
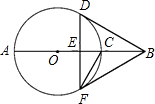 如图,AB经过⊙O的圆心,弦DF⊥AB于E,BF切⊙O于F,⊙O的半径为2.
如图,AB经过⊙O的圆心,弦DF⊥AB于E,BF切⊙O于F,⊙O的半径为2.
(1)求证:BD与⊙O相切;
(2)若∠ABD=∠DFC,求DF的长.
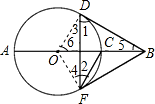 (1)证明:连接OD,OF.
(1)证明:连接OD,OF.∵BF切⊙O于点F,
∴∠OFB=90°,
∵弦DF⊥AB于E,且AB经过圆心O,
∴DE=EF,
∴BD=BF.
∴∠1=∠BFD.
∵OD=OF,
∴∠3=∠4,
∴∠ODB=∠OFB=90°,
∴BD与⊙O相切;
(2)解:由(1)可知∠3=∠5,
∵∠2=∠5,
∴∠2=∠3.
又∵∠6=2∠2,
∴∠6=2∠3.
∵∠6+∠3=90°,
∴3∠3=90°.
∴∠3=30°,
∵OD=2,
∴DE=
 ,
,∴DF=2
 .
.分析:(1)连接OD,OF,根据BF切⊙O于点F,得出∠OFB=90°,再根据弦DF⊥AB于E,且AB经过圆心O,得出∠1=∠BFD,最后根据OD=OF,∠3=∠4,得出∠ODB=∠OFB=90°即可;
(2)根据(1)得∠3=∠5,根据∠2=∠5,得出∠2=∠3,再根据∠6=2∠2,得出∠6=2∠3,再根据∠6+∠3=90°,求出∠3的度数,最后根据⊙O的半径为2,即可求出DF的长.
点评:此题考查了切线的判定与性质,用到的知识点是垂径定理,圆心角与圆周角之间的关系,圆的有关性质等,解题的关键是证出∠ODB=∠OFB=90°,难度适中.

练习册系列答案
相关题目
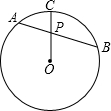
 (1998•河北)已知:如图弦AB经过⊙O的半径OC的中点P,且AP=2,PB=3,则是⊙O的半径等于( )
(1998•河北)已知:如图弦AB经过⊙O的半径OC的中点P,且AP=2,PB=3,则是⊙O的半径等于( )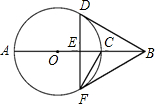 (2007•海淀区二模)如图,AB经过⊙O的圆心,弦DF⊥AB于E,BF切⊙O于F,⊙O的半径为2.
(2007•海淀区二模)如图,AB经过⊙O的圆心,弦DF⊥AB于E,BF切⊙O于F,⊙O的半径为2.