题目内容
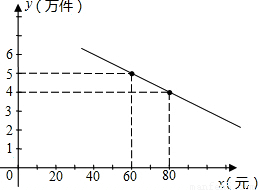
某通讯器材公司销售一种市场需求较大的新型通讯产品.已知每件产品的进价为40元,每年销售该种产品的总开支(不含进价)总计120万元.在销售过程中发现,年销售量y(万件)随销售单价x(元)增大而减小,且年销售量y(万件)与销售单价x(元)之间存在着一次函数关系y=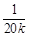 x+b,其中整数k使式子
x+b,其中整数k使式子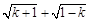 有意义.经测算,销售单价为60元时,年销售量为50000件.
有意义.经测算,销售单价为60元时,年销售量为50000件.【小题1】求y与x的函数关系式;
【小题2】试写出该公司销售该产品的年获利z(万元)关于销售单价x(元)的函数关系式(年获利=年销售额―年销售产品总进价―年总开支).当销售单价x为何值时,年获利最大?并求这个最大值;
【小题3】若公司希望该种产品一年的销售获利不低于40万元.请你帮助该公司确定销售单价的范围.在此情况下,要使产品销售量最大,你认为销售单价应定为多少元?
【小题1】y=
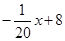
【小题2】60
【小题3】80元解析:
(1)使式子
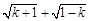 有意义必须k只能等于-1,代入y=
有意义必须k只能等于-1,代入y= x+b,得y=
x+b,得y= 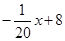
(2) z=yx-40y-120=(-
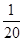 x+8)(x-40)-120-
x+8)(x-40)-120- 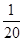
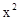 +10x-440=-
+10x-440=-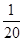
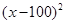 +60
+60(3)∴当x=100元时,年获利最大值为60万元令z=40,得40="-"
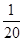
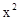 +10x-440整理得
+10x-440整理得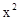 -200x+9600=0
-200x+9600=0解得:
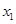 =80,
=80,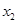 =120.要使年获利不低于40万元,销售单价应在80元到120元之间, 又因为销售单价越低,销售量越大,所以要使销售量最大,又要使年获利不低于40万元,则销售单价应定为80元
=120.要使年获利不低于40万元,销售单价应在80元到120元之间, 又因为销售单价越低,销售量越大,所以要使销售量最大,又要使年获利不低于40万元,则销售单价应定为80元 
练习册系列答案
相关题目
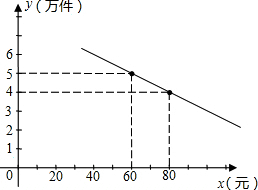 你帮助该公司确定销售单价的范围.在此情况下,要使产品销售量最大,你认为销售单价应定为多少元?
你帮助该公司确定销售单价的范围.在此情况下,要使产品销售量最大,你认为销售单价应定为多少元?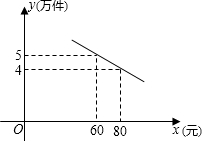 售量y(万件)与销售单价x(元)之间存在如图所示的一次函数关系.
售量y(万件)与销售单价x(元)之间存在如图所示的一次函数关系.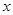 元.(
元.(