题目内容
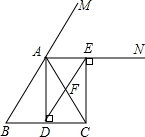 已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为E,连接DE交AC于F
已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为E,连接DE交AC于F(1)求证:四边形ADCE为矩形;
(2)求证:DF∥AB,DF=
| 1 | 2 |
分析:(1)由AB=AC,得∠B=∠ACB,又有外角及角平分线的性质可得AN∥BC,再由垂直关系即可得出结论.
(2)由矩形的对角线相等且互相平分,得出∠FDC=∠FCD=∠B,即可DF∥AB,再由中位线定理可得DF=
AB.
(2)由矩形的对角线相等且互相平分,得出∠FDC=∠FCD=∠B,即可DF∥AB,再由中位线定理可得DF=
| 1 |
| 2 |
解答: 证明:(1)∵AB=AC,AD⊥BC,
证明:(1)∵AB=AC,AD⊥BC,
∴∠BAD=∠CAD,∠ABC=∠ACB,
又∠MAC=∠ABC+∠ACB=2∠ACB,
又AN平分∠MAC,
∴∠NAC=∠MAN=∠ACB,
∵∠MAN+∠CAN+∠BAD+∠CAD=180°,
∴∠DAE=∠CAD+∠CAN=
×180°=90°,
又CE⊥AN,AD⊥BC,
∴∠ADC=∠AEC=90°,
∴四边形ADCE为矩形;
(2)∵四边形ADCE为矩形,
∴∠FDC=∠FCD,
∴∠FDC=∠B,
∴DF∥AB,
∵D是BC的中点,F是AC的中点,
∴在△ABC中,DF=
AB.
 证明:(1)∵AB=AC,AD⊥BC,
证明:(1)∵AB=AC,AD⊥BC,∴∠BAD=∠CAD,∠ABC=∠ACB,
又∠MAC=∠ABC+∠ACB=2∠ACB,
又AN平分∠MAC,
∴∠NAC=∠MAN=∠ACB,
∵∠MAN+∠CAN+∠BAD+∠CAD=180°,
∴∠DAE=∠CAD+∠CAN=
| 1 |
| 2 |
又CE⊥AN,AD⊥BC,
∴∠ADC=∠AEC=90°,
∴四边形ADCE为矩形;
(2)∵四边形ADCE为矩形,
∴∠FDC=∠FCD,
∴∠FDC=∠B,
∴DF∥AB,
∵D是BC的中点,F是AC的中点,
∴在△ABC中,DF=
| 1 |
| 2 |
点评:本题主要考查了平行线的判定及三角形外角的性质和角平分线的性质等,能够掌握并熟练运用.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案
相关题目
 34、已知:如图,在AB、AC上各取一点,E、D,使AE=AD,连接BD,CE,BD与CE交于O,连接AO,∠1=∠2,
34、已知:如图,在AB、AC上各取一点,E、D,使AE=AD,连接BD,CE,BD与CE交于O,连接AO,∠1=∠2, (2013•启东市一模)已知,如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC边于D.
(2013•启东市一模)已知,如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC边于D. 已知:如图,在△ABC中,∠C=120°,边AC的垂直平分线DE与AC、AB分别交于点D和点E.
已知:如图,在△ABC中,∠C=120°,边AC的垂直平分线DE与AC、AB分别交于点D和点E. 已知:如图,在AB、AC上各取一点E、D,使AE=AD,连接BD,CE,BD与CE交于O,连接AO,∠1=∠2,
已知:如图,在AB、AC上各取一点E、D,使AE=AD,连接BD,CE,BD与CE交于O,连接AO,∠1=∠2,