ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩΓΑ―ο÷ίΤαΤςΓ±Οϊ―οΧλœ¬Θ§Ρ≥ΆχΒξΉ®Ο≈œζ έΡ≥÷÷ΤΖ≈ΤΒΡΤαΤς± Ά≤Θ§≥…±ΨΈΣ![]() ‘Σ/ΦΰΘ§ΟΩΧλœζ έ
‘Σ/ΦΰΘ§ΟΩΧλœζ έ![]() Θ®ΦΰΘ©”κœζ έΒΞΦέ
Θ®ΦΰΘ©”κœζ έΒΞΦέ![]() Θ®‘ΣΘ©÷°Φδ¥φ‘Ύ“Μ¥ΈΚ· ΐΙΊœΒΘ§»γΆΦΥυ Ψ.
Θ®‘ΣΘ©÷°Φδ¥φ‘Ύ“Μ¥ΈΚ· ΐΙΊœΒΘ§»γΆΦΥυ Ψ.

Θ®1Θ©«σ![]() ”κ
”κ![]() ÷°ΦδΒΡΚ· ΐΙΊœΒΘΜ
÷°ΦδΒΡΚ· ΐΙΊœΒΘΜ
Θ®2Θ©»γΙϊΙφΕ®ΟΩΧλΤαΤς± Ά≤ΒΡœζ έΝΩ≤ΜΒΆ”Ύ![]() ΦΰΘ§Β±œζ έΒΞΦέΈΣΕύ…Ό‘Σ ±Θ§ΟΩΧλΜώ»ΓΒΡάϊ»σΉν¥σΘ§Ήν¥σάϊ»σ «Εύ…ΌΘΩ
ΦΰΘ§Β±œζ έΒΞΦέΈΣΕύ…Ό‘Σ ±Θ§ΟΩΧλΜώ»ΓΒΡάϊ»σΉν¥σΘ§Ήν¥σάϊ»σ «Εύ…ΌΘΩ
Θ®3Θ©ΗΟΆχΒξΒξ÷ς»»–ΡΙΪ“φ ¬“ΒΘ§ΨωΕ®¥”ΟΩΧλΒΡœζ έάϊ»σ÷–Ψη≥ω150‘ΣΗχœΘΆϊΙΛ≥ΧΘ§ΈΣΝΥ±Θ÷ΛΨηΩνΚσΟΩΧλ Θ”ύάϊ»σ≤ΜΒΆ”Ύ![]() ‘ΣΘ§ ‘»ΖΕ®ΗΟΤαΤς± Ά≤œζ έΒΞΦέΒΡΖΕΈß.
‘ΣΘ§ ‘»ΖΕ®ΗΟΤαΤς± Ά≤œζ έΒΞΦέΒΡΖΕΈß.
ΓΨ¥πΑΗΓΩΘ®1Θ©![]() ΘΜΘ®2Θ©œζ έΒΞΦέΈΣ44‘Σ ±Θ§ΟΩΧλΜώ»ΓΒΡάϊ»σΉν¥σΘ§
ΘΜΘ®2Θ©œζ έΒΞΦέΈΣ44‘Σ ±Θ§ΟΩΧλΜώ»ΓΒΡάϊ»σΉν¥σΘ§![]() ‘ΣΘΜΘ®3Θ©
‘ΣΘΜΘ®3Θ©![]() .
.
ΓΨΫβΈωΓΩ
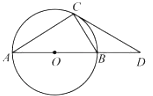
Θ®1Θ©Ω…”Ο¥ΐΕ®œΒ ΐΖ®ά¥»ΖΕ®y”κx÷°ΦδΒΡΚ· ΐΙΊœΒ ΫΘΜ
Θ®2Θ©ΗυΨίάϊ»σ=œζ έΝΩΓΝΒΞΦΰΒΡάϊ»σΘ§»ΜΚσΫΪΘ®1Θ©÷–ΒΡΚ· ΐ Ϋ¥ζ»κΤδ÷–Θ§«σ≥ωάϊ»σΚΆœζ έΒΞΦΰ÷°ΦδΒΡΙΊœΒ ΫΘ§»ΜΚσΗυΨίΤδ–‘÷ ά¥≈–Εœ≥ωΉν¥σάϊ»σΘΜ
Θ®3Θ© Ήœ»ΒΟ≥ωw”κxΒΡΚ· ΐΙΊœΒ ΫΘ§ΫχΕχάϊ”ΟΥυΜώάϊ»σΒ»”Ύ3490‘Σ ±Θ§Ε‘”ΠxΒΡ÷ΒΘ§ΗυΨί‘ωΦθ–‘Θ§«σ≥ωxΒΡ»Γ÷ΒΖΕΈßΘ°
Θ®1Θ©…η![]()
![]() Ψ≠ΙΐΒψ
Ψ≠ΙΐΒψ![]()
![]()
ΫβΒΟ![]()
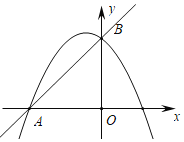
Ι y”κxΒΡΙΊœΒ ΫΈΣΘΚ![]()
Θ®2Θ©30ΘΦ![]()
…ηάϊ»σΈΣ![]()
![]()
![]()
Γύx<50 ±Θ§wΥφxΒΡ‘ω¥σΕχ‘ω¥σΘ§
ΓύΒ±![]() ±Θ§
±Θ§![]()
Θ®2Θ©”…Χβ“βΘ§ΒΟ
-10x+700Γί260Θ§
ΫβΒΟxΓή44Θ§
Γύ30ΘΦxΓή44Θ§
…ηάϊ»σΈΣw=Θ®x-30Θ©y=Θ®x-30Θ©Θ®-10x+700Θ©Θ§
w=-10x2+1000x-21000=-10Θ®x-50Θ©2+4000Θ§
ΓΏ-10ΘΦ0Θ§
ΓύxΘΦ50 ±Θ§wΥφxΒΡ‘ω¥σΕχ‘ω¥σΘ§
Γύx=44 ±Θ§wΉν¥σ=-10Θ®44-50Θ©2+4000=3640Θ§
¥πΘΚΒ±œζ έΒΞΦέΈΣ44‘Σ ±Θ§ΟΩΧλΜώ»ΓΒΡάϊ»σΉν¥σΘ§Ήν¥σάϊ»σ «3640‘ΣΘΜ
Θ®3Θ©w-150=-10x2+1000x-21000-150=3490Θ§
-10Θ®x-50Θ©2=-360Θ§
x-50=Γά6Θ§
x1=56Θ§x2=44Θ§
»γΆΦΥυ ΨΘ§”…ΆΦœσΒΟΘΚ
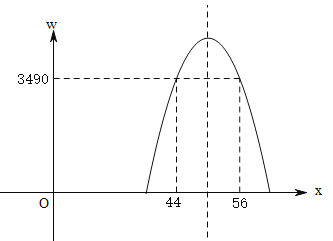
Β±44ΓήxΓή56 ±Θ§ΨηΩνΚσΟΩΧλ Θ”ύάϊ»σ≤ΜΒΆ”Ύ3490‘ΣΘ°

 ’ψ¥σ”≈―ß–Γ―ßΡξΦΕœΈΫ”ΫίΨΕ’ψΫ≠¥σ―ß≥ωΑφ…γœΒΝ–¥πΑΗ
’ψ¥σ”≈―ß–Γ―ßΡξΦΕœΈΫ”ΫίΨΕ’ψΫ≠¥σ―ß≥ωΑφ…γœΒΝ–¥πΑΗΓΨΧβΡΩΓΩΡ≥–ΘΨΌ––ΝΥ¥¥Ϋ®»ΪΙζΈΡΟς≥« –÷Σ ΕΨΚ»ϋΜνΕ·Θ§≥θ“ΜΡξΦΕ»ΪΧεΆ§―ß≤ΈΦ”ΝΥΨΚ»ϋ. ’Φ· ΐΨίΘΚœ÷ΥφΜζ≥ι»Γ≥θ“ΜΡξΦΕ30ΟϊΆ§―ßΓΑ¥¥ΈΡ÷Σ ΕΨΚ»ϋΓ±≥…Φ®Θ§Ζ÷ ΐ»γœ¬Θ®ΒΞΈΜΘΚΖ÷Θ©ΘΚ
90 | 85 | 68 | 92 | 81 | 84 | 95 | 93 | 87 | 89 | 78 | 99 | 89 | 85 | 97 |
88 | 81 | 95 | 86 | 98 | 95 | 93 | 89 | 86 | 84 | 87 | 79 | 85 | 89 | 82 |
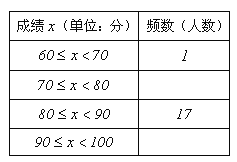

Δ≈«κΫΪΆΦ±μ÷–Ω’»±ΒΡ≤ΩΖ÷≤Ι≥δΆξ’ϊΘΜ
ΔΤ―ß–ΘΨωΕ®±μ’ΟΓΑ¥¥ΈΡ÷Σ ΕΨΚ»ϋΓ±≥…Φ®‘Ύ90Ζ÷“‘…œΒΡΆ§―ßΘ§ΗυΨί…œ±μΆ≥ΦΤΫαΙϊΙάΦΤΗΟ–Θ≥θ“ΜΡξΦΕ360»Υ÷–Θ§‘Φ”–Εύ…Ό»ΥΫΪΜώΒΟ±μ’ΟΘΜ
Δ«ΓΑ¥¥ΈΡ÷Σ ΕΨΚ»ϋΓ±÷–Θ§ ήΒΫ±μ’ΟΒΡ–ΓΚλΆ§―ßΒΟΒΫΝΥ”Γ”–Ι®…»ΓΔΦτ÷ΫΓΔ≤ ΒΤΓΔΩ÷ΝζΆΦΑΗΒΡΥΡΟΕΦΆΡν’¬Θ§Υΐ¥”÷–―Γ»ΓΝΫΟΕΥΆΗχΒήΒήΘ§‘ρ–ΓΚλΥΆΗχΒήΒήΒΡΝΫΟΕΦΆΡν’¬÷–Θ§«ΓΚΟ”–Ω÷ΝζΆΦΑΗΒΡΗ≈¬ « .