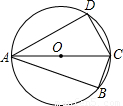
题目内容
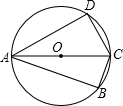 已知:如图,面积为2的四边形ABCD内接于⊙O,对角线AC经过圆心,若∠BAD=45°,CD=
已知:如图,面积为2的四边形ABCD内接于⊙O,对角线AC经过圆心,若∠BAD=45°,CD=| 2 |
分析:延长BC、AD交于点E.可得等腰直角三角形ABE和等腰直角三角形DEC,设AB为x,则BC=x-2,CE=2,DE=
,AD=
x-
,由四边形ABCD面积为2得
×
(
x-
)+
x(x-2)=2,解得x=
,即求AB的长.
| 2 |
| 2 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
| 2 |
| 1 |
| 2 |
| 6 |
解答: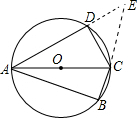 解:延长BC、AD交于点E.
解:延长BC、AD交于点E.
∵∠BAD=45°,
∴△ABE和△DEC是等腰直角三角形.
∵CD=
,
设AB为x,
则BC=x-2,CE=2,DE=
,AD=
x-
.
∵四边形ABCD面积为2,
∴
×
(
x-
)+
x(x-2)=2,
解得x=
.
即AB=
.
 解:延长BC、AD交于点E.
解:延长BC、AD交于点E.∵∠BAD=45°,
∴△ABE和△DEC是等腰直角三角形.
∵CD=
| 2 |
设AB为x,
则BC=x-2,CE=2,DE=
| 2 |
| 2 |
| 2 |
∵四边形ABCD面积为2,
∴
| 1 |
| 2 |
| 2 |
| 2 |
| 2 |
| 1 |
| 2 |
解得x=
| 6 |
即AB=
| 6 |
点评:把有一个直角的四边形添加辅助线转化成直角三角形来解.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
 ,则AB的长等于 .
,则AB的长等于 .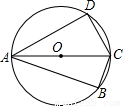
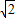 ,则AB的长等于 .
,则AB的长等于 .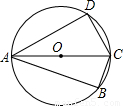
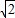 ,则AB的长等于 .
,则AB的长等于 .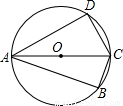
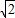 ,则AB的长等于 .
,则AB的长等于 .