Question

（本小题满分12分）如图，在平面直角坐标系中，直线：与轴交于点，与轴交于点，抛物线过点、点，且与轴的另一交点为，其中＞0，又点是抛物线的对称轴上一动点．

（1）求点的坐标，并在图1中的上找一点，使到点与点的距离之和最小；

（2）若△周长的最小值为，求抛物线的解析式及顶点的坐标；

（3）如图2，在线段上有一动点以每秒2个单位的速度从点向点移动(不与端点、重合)，过点作∥交轴于点,设移动的时间为秒，试把△的面积表示成时间的函数，当为何值时，有最大值，并求出最大值.

 

Answer 1

见解析

解析:（1）由题意直线AC与x轴的交点为A，

所以当y=0，则x=﹣6，

所以点A（﹣6，0）．

同理点C（0，8），

由题意，A、B是抛物线y=ax²+bx+8与x轴的交点，

∴﹣6，x₀是一元二次方程ax²+bx+8=0的两个根，

∴﹣6+x₀=﹣，﹣6x₀=，

∴a=﹣，b=﹣+．

∵A、B点关于抛物线对称，∴BC所在直线与对称轴的交点即为P₀．

设直线BC的解析式为y=mx+n，则n=8，mx₀+n=0，

∴m=﹣，n=8．

∴BC的解析式为y=﹣x+8．

∴当x=﹣=时，y=+4，

∴P₀的坐标为（，+4）；

（2）由（1）可知三角形PAC最小即为AC+BC=10，

+=10，

解得x₀=10或x₀=﹣10（不符舍去），

则点B（10，0），

由点A，B，C三点的二次函数式为y==﹣（x﹣2）²+．

顶点N（2，）；

（3）如图，作MN⊥BC于点N，

则△OBC∽△NCM，

所以=，

即h=．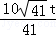

因为MH∥BC，

所以，

解得MH==，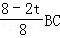

S=MHh，

=×（8﹣2t）×，

=10t﹣，

因为每秒移动2个单位，

则当t=2时符合范围0＜t＜4，

所以当t为2时S最大为10；