题目内容
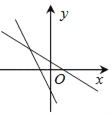
【题目】已知直线y=﹣ ![]() x+3与x轴、y轴分别交于A、B两点,设O为坐标原点.
x+3与x轴、y轴分别交于A、B两点,设O为坐标原点.
(1)求∠ABO的正切值;
(2)如果点A向左平移12个单位到点C,直线l过点C且与直线y=﹣ ![]() x+3平行,求直线l的解析式.
x+3平行,求直线l的解析式.
【答案】
(1)
解:∵直线y=﹣ ![]() x+3与x轴、y轴分别交于A、B两点,
x+3与x轴、y轴分别交于A、B两点,
∴A(6,0),B(0,3),
∴OA=6,OB=3,
∵∠AOB=90°,
∴tan∠ABO= ![]() =
= ![]() =2;
=2;
(2)
解:将点A向左平移12个单位到点C,
∴C(﹣6,0),
∵直线l过点C且与直线y=﹣ ![]() x+3平行,
x+3平行,
设直线l的解析式为y=﹣ ![]() x+b,
x+b,
把C(﹣6,0)代入y=﹣ ![]() x+b得0=﹣
x+b得0=﹣ ![]() (﹣6)+b,
(﹣6)+b,
∴b=﹣3,
∴直线l的解析式为y=﹣ ![]() x﹣3.
x﹣3.
【解析】(1)根据已知条件得到A(6,0),B(0,3),求得OA=6,OB=3,根据三角函数的定义即可得到结论;(2)将点A向左平移12个单位到点C,于是得到C(﹣6,0),设直线l的解析式为y=﹣ ![]() x+b,把C(﹣6,0)代入y=﹣
x+b,把C(﹣6,0)代入y=﹣ ![]() x+b即可得到结论.
x+b即可得到结论.
【考点精析】本题主要考查了坐标与图形变化-平移和解直角三角形的相关知识点,需要掌握新图形的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点;连接各组对应点的线段平行且相等;解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法)才能正确解答此题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目