题目内容
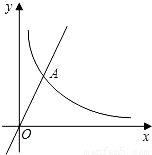
(2012•河源)已知图中的曲线函数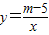 (m为常数)图象的一支.
(m为常数)图象的一支.(1)求常数m的取值范围;
(2)若该函数的图象与正比例函数y=2x图象在第一象限的交点为A(2,n),求点A的坐标及反比例函数的解析式.

【答案】分析:(1)曲线函数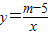 (m为常数)图象的一支.在第一象限,则比例系数m-5一定大于0,即可求得m的范围;
(m为常数)图象的一支.在第一象限,则比例系数m-5一定大于0,即可求得m的范围;
(2)把A的坐标代入正比例函数解析式,即可求得A的坐标,再代入反比例函数解析式即可求得反比例函数解析式.
解答:解:(1)根据题意得:m-5>0,解得:m>5;
(2)根据题意得:n=4,把(2,4)代入函数 ,得到:4=
,得到:4=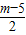 ;
;
解得:m-5=8.
则反比例函数的解析式是y=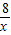 .
.
点评:本题考查了反比例函数的性质及与一次函数的交点问题,综合性较强,同学们要熟练掌握.
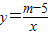 (m为常数)图象的一支.在第一象限,则比例系数m-5一定大于0,即可求得m的范围;
(m为常数)图象的一支.在第一象限,则比例系数m-5一定大于0,即可求得m的范围;(2)把A的坐标代入正比例函数解析式,即可求得A的坐标,再代入反比例函数解析式即可求得反比例函数解析式.
解答:解:(1)根据题意得:m-5>0,解得:m>5;
(2)根据题意得:n=4,把(2,4)代入函数
 ,得到:4=
,得到:4=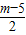 ;
;解得:m-5=8.
则反比例函数的解析式是y=
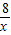 .
.点评:本题考查了反比例函数的性质及与一次函数的交点问题,综合性较强,同学们要熟练掌握.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
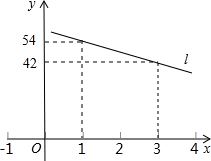 次加满油后,油箱内的余油量y(升)与行驶时间x(小时)的函数关系的图象如图所示的直线l上的一部分.
次加满油后,油箱内的余油量y(升)与行驶时间x(小时)的函数关系的图象如图所示的直线l上的一部分.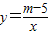 (m为常数)图象的一支.
(m为常数)图象的一支.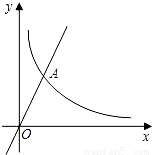
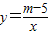 (m为常数)图象的一支.
(m为常数)图象的一支.