题目内容
 如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴相交于点C.连接AC,BC,A(-3,0),C(0,
如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴相交于点C.连接AC,BC,A(-3,0),C(0,| 3 |
(1)求抛物线的解析式;
(2)若点M、N同时从B点出发,均以每秒1个单位长度的速度分别沿BA、BC边运动,其中一个点到达终点时,另一点也随之停止运动.
①当运动时间为t秒时,连接MN,将△BMN沿MN翻折,B点恰好落在AC边上的P处,求t的值及点P的坐标;
②抛物线的对称轴上是否存在点Q,使得以B、N、Q为顶点的三角形与△A0C相似?如果存在,请直接写出点Q的坐标;如果不存在,请说明理由.
③当运动时间为t秒时,连接MN,将△BMN沿MN翻折,得到△PMN.并记△PMN与△AOC的重叠部分的面积为S.求S与t的函数关系式.
分析:(1)此题的关键是求出三个待定系数,首先由“当x=-4和x=2时二次函数的函数值y相等”确定抛物线的对称轴,进而能求出a、b间的数量关系,由C点坐标不难得出c的值,再代入A点坐标后即可得解.
(2)①由(1)的结果不难得出B点的坐标,此时可以发现△ABC恰好是一个含30°角的特殊直角三角形,即∠ABC=60°,因此△BMN是一个等边三角形,而四边形BNPM是一个菱形,即BM=BN=PN=t,由于PN∥AB,根据平行线分线段成比例定理可列出关于PN、AB、CN、CB的比例关系式,根据此时可求出t的值;
在求点P的坐标时,首先要求出直线AC的解析式,点P的纵坐标可由△BNM的高得出,则P点坐标不难求出.
②在①中,已经得到了△ABC的特殊形状,显然△AOC的形状和△ABC是完全一样的,所以若以B、N、Q为顶点的三角形与△AOC相似,那么△BNQ也必须是一个含30°角的直角三角形,所以可以分两种情况讨论:
Ⅰ、∠BNQ是直角,由于∠NBM是60°,那么点Q必须在x轴上,即点Q为抛物线对称轴与x轴的交点;
Ⅱ、∠NBQ是直角,此时BQ∥AC,即两条直线的斜率相等,首先求出直线BQ的解析式,联立抛物线对称轴方程即可得到Q点的坐标.
③此题需要注意三个关键位置:P落在y轴上时(设此时t=α)、点M和点O重合时(设此时t=β)、P落在AC上时(设此时t=γ),那么整体上可以分四段:
Ⅰ、0<t≤α时,△PMN和△AOC不重合,S=0;
Ⅱ、α<t≤β时(参照解答部分③-Ⅱ图),△PMN和△AOC的重合部分是个含30°角的小直角三角形,首先在Rt△BOC中由平行线分线段成比例定理求出GH的表达式,进而得出PG的长,而GH=
PG,则△PGH的面积(即S)可求;
Ⅲ、β<t≤γ时(参照解答部分③-Ⅲ图),△PMN和△AOC的重合部分是个不规则图形,其面积可由△PMN的面积(即△BMN的面积)减去含30°角的小直角三角形得出;
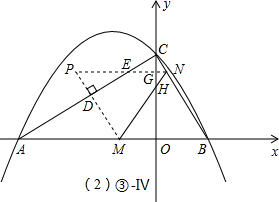
Ⅳ、γ<t≤2时(参照解答部分③-Ⅳ图),△PMN和△AOC的重合部分是个不规则图形,其面积可由△PMN的面积(即△BMN的面积)减去两个含30°角的小直角三角形得出.
(2)①由(1)的结果不难得出B点的坐标,此时可以发现△ABC恰好是一个含30°角的特殊直角三角形,即∠ABC=60°,因此△BMN是一个等边三角形,而四边形BNPM是一个菱形,即BM=BN=PN=t,由于PN∥AB,根据平行线分线段成比例定理可列出关于PN、AB、CN、CB的比例关系式,根据此时可求出t的值;
在求点P的坐标时,首先要求出直线AC的解析式,点P的纵坐标可由△BNM的高得出,则P点坐标不难求出.
②在①中,已经得到了△ABC的特殊形状,显然△AOC的形状和△ABC是完全一样的,所以若以B、N、Q为顶点的三角形与△AOC相似,那么△BNQ也必须是一个含30°角的直角三角形,所以可以分两种情况讨论:
Ⅰ、∠BNQ是直角,由于∠NBM是60°,那么点Q必须在x轴上,即点Q为抛物线对称轴与x轴的交点;
Ⅱ、∠NBQ是直角,此时BQ∥AC,即两条直线的斜率相等,首先求出直线BQ的解析式,联立抛物线对称轴方程即可得到Q点的坐标.
③此题需要注意三个关键位置:P落在y轴上时(设此时t=α)、点M和点O重合时(设此时t=β)、P落在AC上时(设此时t=γ),那么整体上可以分四段:
Ⅰ、0<t≤α时,△PMN和△AOC不重合,S=0;
Ⅱ、α<t≤β时(参照解答部分③-Ⅱ图),△PMN和△AOC的重合部分是个含30°角的小直角三角形,首先在Rt△BOC中由平行线分线段成比例定理求出GH的表达式,进而得出PG的长,而GH=
| 3 |
Ⅲ、β<t≤γ时(参照解答部分③-Ⅲ图),△PMN和△AOC的重合部分是个不规则图形,其面积可由△PMN的面积(即△BMN的面积)减去含30°角的小直角三角形得出;
Ⅳ、γ<t≤2时(参照解答部分③-Ⅳ图),△PMN和△AOC的重合部分是个不规则图形,其面积可由△PMN的面积(即△BMN的面积)减去两个含30°角的小直角三角形得出.
解答:解:(1)∵当x=-4和x=2时二次函数的函数值y相等,
∴抛物线对称轴:x=-
=-1,即b=2a;
由C(0,
)得:c=
;
将A(-3,0)代入y=ax2+2ax+
(a≠0)中,得:
9a-6a+
=0,a=-
∴抛物线的解析式:y=-
x2-
x+
.
(2)由(1)的抛物线解析式知:A(-3,0)、B(1,0)、C(0,
),则:
OA=3,OB=1,OC=
,即 OC2=OA•OB,又OC⊥AB,则△ABC是直角三角形,且∠CAB=30°,∠ABC=60°;
①△BMN中,BM=BN=t,∠NBM=60°,即△BNM是等边三角形;
由于△PMN由△BMNA翻转所得,所以△PMN也是等边三角形,四边形PNBM是菱形;
∴PN∥AB(如题干图),得:
=
,代入数据,有:
=
,解得:t=
;
由tan∠CAO=
、C(0,
)得,直线AC:y=
x+
;
当y=t•sin60°=
时,
x+
=
,x=-1
即 P(-1,
);
综上,B点恰好落在AC边上的P处时,t=
,P(-1,
).
②∵△AOC是一个含30°角的直角三角形,
∴若以B、N、Q为顶点的三角形与△A0C相似,那么△BNQ也必须是一个含30°角的直角三角形.
分三种情况讨论:
Ⅰ、∠QNB=90°、∠BQN=30°(如②-Ⅰ图);
∵∠ABC=∠Q1BN=60°,∴点Q1在x轴上,即Q1(-1,0);
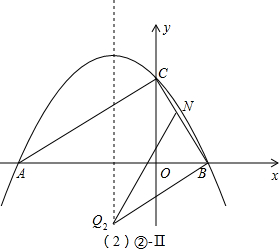
Ⅱ、∠QBN=90°、∠BQN=30°(如②-Ⅱ图);
此时BQ2∥AC,设直线BQ2:y=
x+b,代入B(1,0),得:b=-
∴直线BQ2:y=
x-
,Q2(-1,-
);
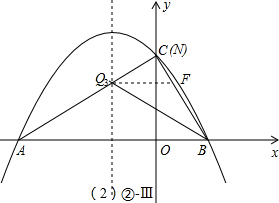
Ⅲ、∠QNB=90°、∠QBN=30°(如②-Ⅲ图);
此时N、C重合,点Q3应在①的P点处,由①的计算结果知:
Q3C=
•sin60°=
,而BC=2,即∠CQ3B=60°,符合条件;
即 Q3(-1,
);
综上,符合条件的Q点的坐标为:Q1(-1,0)、Q2(-1,-
)、Q3(-1,
).
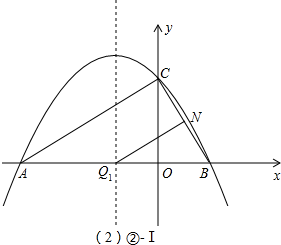
③当点P落在y轴上时,
=
,即
=
,解得:t=
;
当点M、O重合时,t=OB=1;
当点P落在AC上时,由①知,t=
;
Ⅰ、当0<t≤
时,△PMN和△AOC不重合,即S=0;
Ⅱ、当
<t≤1时(如③-Ⅱ图),由
=
可求得:GN=1-
,PG=PN-GN=t-(1-
)=
-1;
S=S△PGH=
×(
-1)×(
-1)
=
(
-1)2;
Ⅲ、当1<t≤
时(如③-Ⅲ图);
由Ⅱ知,GN=1-
,GH=
GN=
(1-
),S△GHN=
×(1-
)×
(1-
)=
t2-
t+
;
S=S△PMN-S△GHN=S△BMN-S△GHN=
×t×
t-(
t2-
t+
)=
t2+
t-
;
Ⅳ、当
<t≤2时(如③-Ⅳ图);
同上,可求得S△PDE=
(
t-2)2=
t2-3
t+2
、S△GHN=
t2-
t+
、S△PMN=
t2,
S=S△PMN-S△PDE-S△GHN=-
t2+
t-
;
综上,S=
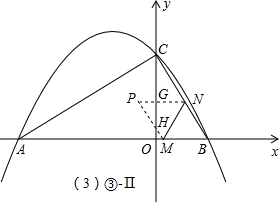
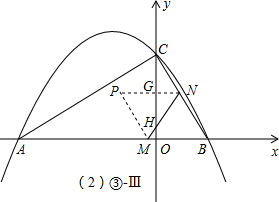
∴抛物线对称轴:x=-
| b |
| 2a |
由C(0,
| 3 |
| 3 |
将A(-3,0)代入y=ax2+2ax+
| 3 |
9a-6a+
| 3 |
| ||
| 3 |
∴抛物线的解析式:y=-
| ||
| 3 |
2
| ||
| 3 |
| 3 |
(2)由(1)的抛物线解析式知:A(-3,0)、B(1,0)、C(0,
| 3 |
OA=3,OB=1,OC=
| 3 |
①△BMN中,BM=BN=t,∠NBM=60°,即△BNM是等边三角形;
由于△PMN由△BMNA翻转所得,所以△PMN也是等边三角形,四边形PNBM是菱形;
∴PN∥AB(如题干图),得:
| PN |
| AB |
| CN |
| BC |
| t |
| 4 |
| 2-t |
| 2 |
| 4 |
| 3 |
由tan∠CAO=
| ||
| 3 |
| 3 |
| ||
| 3 |
| 3 |
当y=t•sin60°=
2
| ||
| 3 |
| ||
| 3 |
| 3 |
2
| ||
| 3 |
即 P(-1,
2
| ||
| 3 |
综上,B点恰好落在AC边上的P处时,t=
| 4 |
| 3 |
2
| ||
| 3 |
②∵△AOC是一个含30°角的直角三角形,
∴若以B、N、Q为顶点的三角形与△A0C相似,那么△BNQ也必须是一个含30°角的直角三角形.
分三种情况讨论:
Ⅰ、∠QNB=90°、∠BQN=30°(如②-Ⅰ图);
∵∠ABC=∠Q1BN=60°,∴点Q1在x轴上,即Q1(-1,0);
Ⅱ、∠QBN=90°、∠BQN=30°(如②-Ⅱ图);
此时BQ2∥AC,设直线BQ2:y=
| ||
| 3 |
| ||
| 3 |
∴直线BQ2:y=
| ||
| 3 |
| ||
| 3 |
2
| ||
| 3 |
Ⅲ、∠QNB=90°、∠QBN=30°(如②-Ⅲ图);
此时N、C重合,点Q3应在①的P点处,由①的计算结果知:
Q3C=
| 4 |
| 3 |
2
| ||
| 3 |
即 Q3(-1,
2
| ||
| 3 |
综上,符合条件的Q点的坐标为:Q1(-1,0)、Q2(-1,-
2
| ||
| 3 |
2
| ||
| 3 |
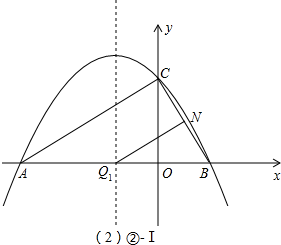


③当点P落在y轴上时,
| PN |
| OB |
| CN |
| BC |
| t |
| 1 |
| 2-t |
| 2 |
| 2 |
| 3 |
当点M、O重合时,t=OB=1;
当点P落在AC上时,由①知,t=
| 4 |
| 3 |
Ⅰ、当0<t≤
| 2 |
| 3 |
Ⅱ、当
| 2 |
| 3 |
| GN |
| OB |
| CN |
| CB |
| t |
| 2 |
| t |
| 2 |
| 3t |
| 2 |
S=S△PGH=
| 1 |
| 2 |
| 3t |
| 2 |
| 3t |
| 2 |
| 3 |
| ||
| 2 |
| 3t |
| 2 |
Ⅲ、当1<t≤
| 4 |
| 3 |
由Ⅱ知,GN=1-
| t |
| 2 |
| 3 |
| 3 |
| t |
| 2 |
| 1 |
| 2 |
| t |
| 2 |
| 3 |
| t |
| 2 |
| ||
| 8 |
| ||
| 2 |
| ||
| 2 |
S=S△PMN-S△GHN=S△BMN-S△GHN=
| 1 |
| 2 |
| ||
| 2 |
| ||
| 8 |
| ||
| 2 |
| ||
| 2 |
| ||
| 8 |
| ||
| 2 |
| ||
| 2 |
Ⅳ、当
| 4 |
| 3 |
同上,可求得S△PDE=
| ||
| 2 |
| 3 |
| 2 |
9
| ||
| 8 |
| 3 |
| 3 |
| ||
| 8 |
| ||
| 2 |
| ||
| 2 |
| ||
| 4 |
S=S△PMN-S△PDE-S△GHN=-
| 3 |
7
| ||
| 2 |
5
| ||
| 2 |
综上,S=
|
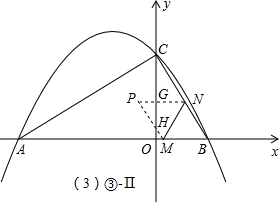
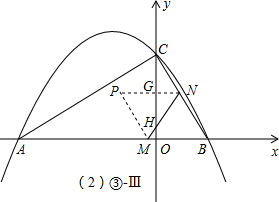

点评:此题主要考查了二次函数解析式的确定、相似三角形的判定和性质以及图形面积的求法;后面两个小题的难度很大,倒数第二道题中,由于涉及到不同的相似情况,是容易漏解的地方;最后一题中,P点的不同位置确定了重合部分的形状,一定要将所有可能的情况画出来,然后根据图形间的面积和差关系来进行解题.

练习册系列答案
 能力评价系列答案
能力评价系列答案
相关题目
 如图,二次函数的图象经过点D(0,
如图,二次函数的图象经过点D(0,
 如图,二次函数y=ax2+bx+c的图象与x轴交于B、C两点,与y轴交于点A(0,-3),∠ABC=45°,∠ACB=60°,求这个二次函数解析式.
如图,二次函数y=ax2+bx+c的图象与x轴交于B、C两点,与y轴交于点A(0,-3),∠ABC=45°,∠ACB=60°,求这个二次函数解析式. 某公司推出了一种高效环保型洗涤用品,年初上市后,公司经历了从亏损到盈利的过程,如图的二次函数图象(部分)刻画了该公司年初以来累积利润s(万元)与时间t(月)之间的关系(即前t个月的利润总和s与t之间的关系).根据图象提供的信息,解答下列问题:
某公司推出了一种高效环保型洗涤用品,年初上市后,公司经历了从亏损到盈利的过程,如图的二次函数图象(部分)刻画了该公司年初以来累积利润s(万元)与时间t(月)之间的关系(即前t个月的利润总和s与t之间的关系).根据图象提供的信息,解答下列问题: 如图,二次函数y=ax2+bx+c的图象与x轴相交于两个点,根据图象回答:(1)b
如图,二次函数y=ax2+bx+c的图象与x轴相交于两个点,根据图象回答:(1)b