题目内容
25、如图，已知等腰梯形ABCD中，AD∥BC，BC-AD=AB，求∠A的度数．分析：过A作AE∥CD交BC于E，得到平行四边形AEDC和等边三角形AEB，推出∠B=60°，根据平行线的性质求出即可．
解答：解：过A作A
E∥CD交BC于E，
∵AD∥BC，DC∥AE，
∴四边形ADCE是平行四边形，
∴AD=CE，AE=CD=AB，
∵BC-AD=AB，
∴BC-EC=BE=AB，
∴△ABE是等边三角形，
∴∠B=60°，
∵AD∥BC，
∴∠BAD=180°-∠B=120°，
答：∠A的度数是120°．
E∥CD交BC于E，∵AD∥BC，DC∥AE，
∴四边形ADCE是平行四边形，
∴AD=CE，AE=CD=AB，
∵BC-AD=AB，
∴BC-EC=BE=AB，
∴△ABE是等边三角形，
∴∠B=60°，
∵AD∥BC，
∴∠BAD=180°-∠B=120°，
答：∠A的度数是120°．
点评：本题主要考查对平行四边形的性质和判定，平行线的性质，等边三角形的性质和判定，等腰梯形的性质等知识点的理解和掌握，能把梯形转化成平行四边形和等边三角形是解此题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
，
3、如图，已知等腰梯形ABCD中，AD∥BC，∠B=60°，AD=2，BC=8，则此等腰梯形的周长为（ ）
如图，已知等腰梯形ABCD中，AD∥BC，BD⊥DC，∠DBC=
13、如图，已知等腰梯形ABCD，AD∥BC，AD=5cm，BC=11cm，高DE=4cm，则梯形的周长为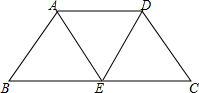
如图，已知等腰梯形ABCD是由三个边长为2的全等的正三角形围成的，则等腰梯形ABCD的面积是