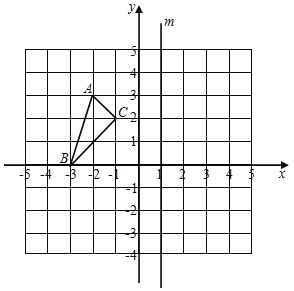
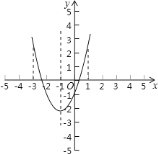
题目内容
【题目】已知△ABC和△ADE都是等腰直角三角形,且∠BAC=∠DAE=90°.
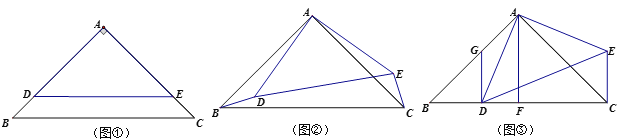
(1)如图①,点D、E分别在线段AB、AC上. 请直接写出线段BD和CE的位置关系: ;
(2)将图①中的△ADE绕点A逆时针旋转到如图②的位置时,(1)中的结论是否成立?若成立,请利用图②证明;若不成立,请说明理由;
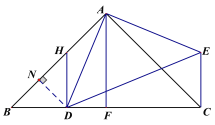
(3)如图③,取BC的中点F,连接AF,当点D落在线段BC上时,发现AD恰好平分∠BAF,此时在线段AB上取一点H,使BH=2DF,连接HD,猜想线段HD与BC的位置关系并证明.
【答案】(1)BD⊥CE;(2)成立,理由见解析;(3)HD⊥BC,证明见解析;
【解析】
(1)根据等腰直角三角形的性质解答;(2)延长延长BD、CE,交于点M,证明△ABD≌△ACE,根据全等三角形的性质、垂直的定义解答;(3)过点D作DN⊥AB于点N,根据题意判定△NDH是等腰直角三角形,从而使问题得解.
解:(1)∵△ABC和△ADE都是等腰直角三角形且点D、E分别在线段AB、AC上,
∴BD⊥CE;
(2)成立
证明:延长BD、CE,交于点M
∵∠BAC=∠DAE=90°
∴∠BAC-∠DAC =∠DAE-∠DAC
即∠BAD=∠CAE
又∵AB=AC,AD=AE
∴△ABD≌△ACE(SAS)
∴∠ABD=∠ACE
在等腰直角△ABC中,∠ABD +∠DBC+∠ACB=90°
∴∠ACE +∠DBC+∠ACB=90°
∴在△MBC中,∠M=180°-(∠ACE +∠DBC+∠ACB)= 90°
∴BD⊥CE
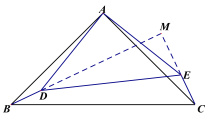
(3)HD⊥BC
证明:过点D作DN⊥AB于点N.
∵AB=AC,BF=CF,
∴AF⊥BC
又∵AD平分∠BAF,且DN⊥AB
∴DN=DF
在Rt△BND中,∠B=45°
∴∠NDB=45°,NB=ND
∴NB=DF
∵BH=2DF
∴BH=2NB
而BH=NB+NH
∴NB=NH=ND
∴△NDH是等腰直角三角形,∠NDH=45°
∴∠HDB=∠NDH +∠NDB= 45°+ 45°=90°
∴HD⊥BC

【题目】己知二次函数![]() 中,函数
中,函数![]() 与自变量
与自变量![]() 的部分对应值如下表:
的部分对应值如下表:
| … |
| 0 | 1 | 2 | 3 | 4 | … |
| … | 10 | 5 | 2 | 1 | 2 | 5 | … |
(1)求该二次函数的解析式;
(2)当![]() 为何值时,
为何值时,![]() 有最小值,最小值是多少?
有最小值,最小值是多少?
(3)若![]() ,
,![]() 两点都在该函数的图像上,试比较
两点都在该函数的图像上,试比较![]() 与
与![]() 的大小.
的大小.