题目内容
已知二次函数y=kx2+(2k-1)x-1与x轴交点的横坐标为x1,x2(x1<x2),则对于下列结论:①当x=-2时,y=1;
②当x>x2时,y>0;
③方程y=kx2+(2k-1)x-1=0有两个不相等的实数根x1,x2;
④x2-x1=
| ||
| k |
其中所有正确的结论是
分析:①把x=2代入函数即可知,②要考虑两种情况k>0和k<0,所以错误,③只要判断△的情况即可,④根据韦达定理即可判断.
解答:解:①把当x=-2代入函数得4k-2(2k-1)-1=1,正确;
②当k<0时,当x>x2时,y<0,错误;
③∵二次函数y=kx2+(2k-1)x-1与x轴有两个不同的交点,
∴方程y=kx2+(2k-1)x-1=0有两个不相等的实数根x1、x2;正确
④x2-x1=
中,k的符号可能为负,应为|k|,错误.
故选①、③.
②当k<0时,当x>x2时,y<0,错误;
③∵二次函数y=kx2+(2k-1)x-1与x轴有两个不同的交点,
∴方程y=kx2+(2k-1)x-1=0有两个不相等的实数根x1、x2;正确
④x2-x1=
| ||
| k |
故选①、③.
点评:本题难度较大,考查了函数与方程的关系,以及根的判别式等内容,需仔细解答.

练习册系列答案
相关题目
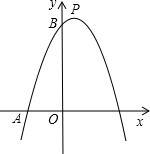 点B,顶点为P,且OB=3OA,一次函数y=kx+b的图象经过点A、点B.
点B,顶点为P,且OB=3OA,一次函数y=kx+b的图象经过点A、点B. 已知二次函数y=ax2+bx+3图象的对称轴为直线x=1.
已知二次函数y=ax2+bx+3图象的对称轴为直线x=1. 为M,又正比例函数y=kx的图象与二次函数相交于两点D、E,且P是线段DE的中点.
为M,又正比例函数y=kx的图象与二次函数相交于两点D、E,且P是线段DE的中点.