题目内容
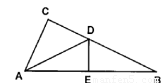
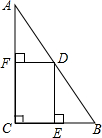如图，点D是Rt△ABC的斜边AB上的一点，DE⊥BC于E，DF⊥AC于F，若AF=15，BE=10，则四边形DECF的面积是分析：易知四边形DECF是矩形，通过证△ADF∽△DBE，可求得DF•DE的值，也就得到了四边形DECF的面积．
解答：解：∵DF⊥AC，DE⊥BC，
∴∠DFC=∠C=∠DEC=90°，
∴四边形DFCE是矩形，
易知DF∥BC，则∠ADF=∠B，
又∵∠AFD=∠DEB，∴△ADF∽△DBE，
∴
=
，即DE•DF=AF•BE=150，
∴S矩形DFCE=DE•DF=150，
即四边形DFCE的面积为150．
∴∠DFC=∠C=∠DEC=90°，
∴四边形DFCE是矩形，
易知DF∥BC，则∠ADF=∠B，
又∵∠AFD=∠DEB，∴△ADF∽△DBE，
∴
| DF |
| BE |
| AF |
| DE |
∴S矩形DFCE=DE•DF=150，
即四边形DFCE的面积为150．
点评：此题主要考查了相似三角形的判定和性质．
练习册系列答案
名校课堂系列答案
相关题目
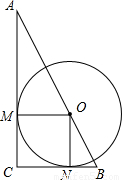
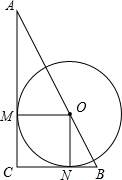如图，点O是Rt△ABC斜边上一点，⊙O与AC，BC分别相切于点M，N．
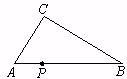10、如图，点P是Rt△ABC斜边AB上的任意一点（A、B两点除外），过点P作一条直线，使截得的三角形与Rt△ABC相似，这样的直线可以作
