题目内容
某商人用7200元购进甲、乙两种商品，然后卖出，若每种商品均用去一半的钱，则一共可购进750件；若用| 2 | 3 |
（1）求甲、乙两种商品的购进价和卖出价；
（2）因市场需求总量有限，每种商品最多只能卖出600件，那么该商人应采取怎样的购货方式才能获得最大的利润？最大利润是多少？
分析：（1）设甲、乙两种商品购进价分别为x元和y元．根据等量关系：①每种商品均用去一半的钱，则一共可购进750件；②用
的钱买甲种商品，其余的钱买乙种商品，则要少购进50件，列方程组求得两种商品的购进价；根据售价=进价×（1+利润率），分别求得两种商品的售价．
（2）要获得最大利润，因为总钱数是一定的，乙商品的利润最大，所以应让乙商品的件数达到最多，即600件，然后求得甲商品的件数，从而求得最大利润．
| 2 |
| 3 |
（2）要获得最大利润，因为总钱数是一定的，乙商品的利润最大，所以应让乙商品的件数达到最多，即600件，然后求得甲商品的件数，从而求得最大利润．
解答：解：（1）设甲、乙两种商品购进价分别为x元和y元．
由题，得
，化简方程组得
，
②×3-①得：
-
=6，解得x=12，
把x=12代入①解得y=8，
所以
经检验，
是原分式方程组的解，
即甲、乙两种商品的购进价分别为12元和8元；
设甲、乙两种商品的卖出价分别为a元和b元．
则：a=12×（1+20%）=14.4元，b=8×（1+25%）=10元，
解得：a=14.4，b=10．
答：甲、乙两种商品的购进价分别为12元和8元，卖出价分别为14.4元和10元；
（2）设购进甲商品m件，那么购进乙商品[（7200-12m）÷8]件，
∴总利润为（14.4-12）m+
×（10-8）=2.4m+1800-3m=-0.6m+1800，
而m≤600，
≤600，
∴200≤m≤600，
∴当m=200，
=600，总利润最多．
∴购进甲商品200件，乙商品600件总利润最多，
总利润为：600（10-8）+200（14.4-12）=1680（元）．
答：购进甲商品200件，乙商品600件才能获得最大利润，最大利润是1680元．
由题，得
|
|
②×3-①得：
| 144 |
| x |
| 72 |
| x |
把x=12代入①解得y=8，
所以
|
经检验，
|
即甲、乙两种商品的购进价分别为12元和8元；
设甲、乙两种商品的卖出价分别为a元和b元．
则：a=12×（1+20%）=14.4元，b=8×（1+25%）=10元，
解得：a=14.4，b=10．
答：甲、乙两种商品的购进价分别为12元和8元，卖出价分别为14.4元和10元；
（2）设购进甲商品m件，那么购进乙商品[（7200-12m）÷8]件，
∴总利润为（14.4-12）m+
| 7200-12m |
| 8 |
而m≤600，
| 7200-12m |
| 8 |
∴200≤m≤600，
∴当m=200，
| 7200-12m |
| 8 |
∴购进甲商品200件，乙商品600件总利润最多，
总利润为：600（10-8）+200（14.4-12）=1680（元）．
答：购进甲商品200件，乙商品600件才能获得最大利润，最大利润是1680元．
点评：分析题意，找到关键描述语，找到合适的等量关系是解决问题的关键．
注意公式：售价=进价×（1+利润率）．
注意公式：售价=进价×（1+利润率）．
练习册系列答案
相关题目
的钱买甲种商品，其余的钱买乙种商品，则要少购进50件，卖出时，甲种商品可盈利20%，乙种商品可盈利25%．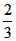
的钱买甲种商品，其余的钱买乙种商品，则要少购进50件，卖出时，甲种商品可盈利20%，乙种商品可盈利25%。求甲、乙两种商品的购进价和卖出价。