题目内容
 已知二次函数y=ax2+bx+c的图象如图,并设M=|a+b+c|-|a-b+c|+|2a+b|-|2a-b|,则( )
已知二次函数y=ax2+bx+c的图象如图,并设M=|a+b+c|-|a-b+c|+|2a+b|-|2a-b|,则( )| A、M>0 | B、M=0 | C、M<0 | D、不能确定M为正、为负或为0 |
分析:由抛物线的位置确定解析式中系数符号特征,判定a、b、c的符号,并由x=±1,推出相应y值的正负性.
解答:解:由图可知a>0,c<0,
对称轴0<-
<1,则b<0,可得2a+b>0,2a-b>0,
当x=1时,a+b+c<0,当x=-1时,a-b+c>0,
且由图可看出|a+b+c|<|a-b+c|,
∴M=|a+b+c|-|a-b+c|+|2a+b|-|2a-b|<0.
故选C.
对称轴0<-
| b |
| 2a |
当x=1时,a+b+c<0,当x=-1时,a-b+c>0,
且由图可看出|a+b+c|<|a-b+c|,
∴M=|a+b+c|-|a-b+c|+|2a+b|-|2a-b|<0.
故选C.
点评:本题看出了二次函数图象与系数的关系,难度一般,在解题中常常要运用图形做出判断,判断出各个参数的正负.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
已知二次函数y=ax+bx+c(a≠0,a,b,c为常数),对称轴为直线x=1,它的部分自变量与函数值y的对应值如下表,写出方程ax2+bx+c=0的一个正数解的近似值________(精确到0.1).
| x | -0.1 | -0.2 | -0.3 | -0.4 |
| y=ax2+bx+c | -0.58 | -0.12 | 0.38 | 0.92 |
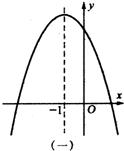 21、已知二次函数y=a(x+1)2+c的图象如图所示,则函数y=ax+c的图象只可能是( )
21、已知二次函数y=a(x+1)2+c的图象如图所示,则函数y=ax+c的图象只可能是( )
