题目内容
【题目】如图,直线AB、CD相交于O点,∠AOC与∠AOD的度数比为4:5,OE⊥AB于点O,OF平分∠DOB,求∠EOF的度数
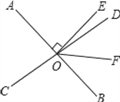
【答案】500
【解析】试题分析:设∠AOC=4x,则∠AOD=5x,根据邻补角的定义得到∠AOC+∠AOD=180°,即4x+5x=180°,解得x=20°,则∠AOC=4x=80°,利用对顶角相等得∠BOD=80°,由OE⊥AB得到∠BOE=90°,则∠DOE=∠BOE-∠BOD=10°,再根据角平分线的定义得到∠DOF= ![]() ∠BOD=40°,利用∠EOF=∠EOD+∠DOF即可得到∠EOF的度数.
∠BOD=40°,利用∠EOF=∠EOD+∠DOF即可得到∠EOF的度数.
试题解析:
设∠AOC=4x,则∠AOD=5x,
∵∠AOC+∠AOD=180°,
∴4x+5x=180°,解得x=20°,
∴∠AOC=4x=80°,
∴∠BOD=80°,
∵OE⊥AB,
∴∠BOE=90°,
∴∠DOE=∠BOE-∠BOD=10°,
又∵OF平分∠DOB,
∴∠DOF= ![]() ∠BOD=40°,
∠BOD=40°,
∴∠EOF=∠EOD+∠DOF=10°+40°=50°.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目