题目内容
（2012•仙居县二模）如图，将两张长为8，宽为2的矩形纸条交叉，重叠部分构成的菱形周长的最大值是17
17
．分析：根据矩形的宽度不变，当两纸条的对角线互相重合时，重叠部分的面积最大，边长也最大，此时设菱形的边长为x，然后表示出BC，再利用勾股定理列式进行计算即可求出x的值，然后根据菱形的周长公式列式进行计算即可得解．
解答：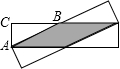
解：如图所示时，重叠部分构成的菱形的周长最大，
设AB=x，
∵矩形纸条的长为8，宽为2，
∴BC=8-x，
在Rt△ABC中，AB2=AC2+BC2，
即x2=22+（8-x）2，
整理得，16x=68，
解得x=
，
故菱形周长的最大值4×
=17．
故答案为：17．
解：如图所示时，重叠部分构成的菱形的周长最大，设AB=x，
∵矩形纸条的长为8，宽为2，
∴BC=8-x，
在Rt△ABC中，AB2=AC2+BC2，
即x2=22+（8-x）2，
整理得，16x=68，
解得x=
| 17 |
| 4 |
故菱形周长的最大值4×
| 17 |
| 4 |
故答案为：17．
点评：本题考查了菱形的性质，利用菱形的面积确定出菱形的边长最大时的情况是解题的关键，还利用了勾股定理．
练习册系列答案
阅读快车系列答案
相关题目
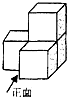（2012•仙居县二模）如图由四个相同的小立方体组成的立体图形，它的主视图是（ ）
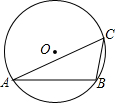（2012•仙居县二模）如图，已知AB是⊙O的弦，C是⊙O上的一个动点，连接AC、BC，∠C=60°，⊙O的半径为2，则△ABC面积的最大值是（ ）