题目内容
在坐标平面中,直线y=x+5分别交x轴、y轴于A、B,直线y=-2x+20分别交x轴、y轴于C、D,直线AB、CD相交于E,
(1)求点E的坐标;
(2)点P为线段AE上的一点,过点P作x轴的平行线分别交直线CB、CD于F、G,设P点的横坐标为m,线段PF的长度为d,求d与m的函数关系式(直接写出自变量m的取值范围);
(3)在(2)的条件下,当直线EF把△BCD的面积分成2:3两部分时,求m的值.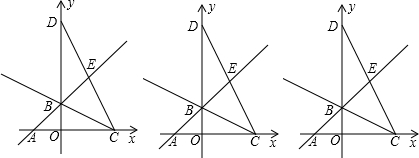
(1)求点E的坐标;
(2)点P为线段AE上的一点,过点P作x轴的平行线分别交直线CB、CD于F、G,设P点的横坐标为m,线段PF的长度为d,求d与m的函数关系式(直接写出自变量m的取值范围);
(3)在(2)的条件下,当直线EF把△BCD的面积分成2:3两部分时,求m的值.

分析:(1)联立两直线解析式,解二元一次方程组即可求出点E的坐标;
(2)先求出点B、C的坐标,再利用待定系数法求出直线BC的解析式,然后分①当点P在线段AB上时,根据点P、F、G的纵坐标相同表示出点P、F的坐标,然后根据PF的长度等于点F的横坐标减去点P的横坐标,计算即可得解;②当点P在线段EB上时,根据点P、F、G的纵坐标相同表示出点P、F的坐标,然后根据PF的长度等于点P的横坐标减去点F的横坐标,计算即可得解;
(3)先求出点D的坐标,再求出点G的坐标,然后表示出FG,然后求出△BCD的面积,再分①点P在AB上时,根据△EFC的面积占2份列式求解即可得到m的值;②点P在EB上时,设EF与y轴的交点为M,根据△DME的面积占2份列式求出DM的长,从而求出点M的坐标,然后求出直线EM的解析式,再与直线BC的解析式联立求解即可得到F的坐标,然后根据与点P的纵坐标相等计算即可求出m的值.
(2)先求出点B、C的坐标,再利用待定系数法求出直线BC的解析式,然后分①当点P在线段AB上时,根据点P、F、G的纵坐标相同表示出点P、F的坐标,然后根据PF的长度等于点F的横坐标减去点P的横坐标,计算即可得解;②当点P在线段EB上时,根据点P、F、G的纵坐标相同表示出点P、F的坐标,然后根据PF的长度等于点P的横坐标减去点F的横坐标,计算即可得解;
(3)先求出点D的坐标,再求出点G的坐标,然后表示出FG,然后求出△BCD的面积,再分①点P在AB上时,根据△EFC的面积占2份列式求解即可得到m的值;②点P在EB上时,设EF与y轴的交点为M,根据△DME的面积占2份列式求出DM的长,从而求出点M的坐标,然后求出直线EM的解析式,再与直线BC的解析式联立求解即可得到F的坐标,然后根据与点P的纵坐标相等计算即可求出m的值.
解答:解:(1)联立
,
解得
.
所以,点E(5,10);
(2)由题意可知B(0,5),C(10,0),
设直线BC的解析式为y=kx+b,则
,
解得
 ,
,
∴直线BC的解析式为y=-
x+5,
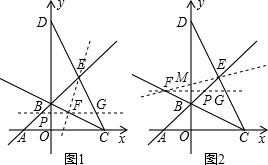
①当点P在线段AB上时(如图1),
∵P、F、G三点具有相同的纵坐标,
∴P(m,m+5),F(-2m,m+5),
∴d=-2m-m=-3m (-5≤m<0),
②当点P在线段EB上时(如图2),
∵P、F、G三点具有相同的纵坐标,
∴P(m,m+5),F(-2m,m+5),
∴d=m-(-2m)=3m(0<m≤5);
(3)D(0,20),G(
,m+5),FG=
-(-2m)=
,
S△DBC=
DB×OC=
×15×10=75,
①如图1,当S△EFC:S△DBC=2:5时,S△EFC=30,
∴S△EFC=
×
×10=30,
∴m=-1,
②如图2,EF交y轴于点M,当S△DME:S△DBC=2:5时,S△DME=30,
∴DM=12∴M(0,8),
可求直线EM的解析式为y=
x+8,
∵
,
∴
,
∴F(-
,
),
∴m+5=
,
∴m=
,
∴当直线EF把△BCD的面积分成2:3两部分时,m的值为-1或
.
|
解得
|
所以,点E(5,10);
(2)由题意可知B(0,5),C(10,0),
设直线BC的解析式为y=kx+b,则
|
解得
|
 ,
,∴直线BC的解析式为y=-
| 1 |
| 2 |
①当点P在线段AB上时(如图1),
∵P、F、G三点具有相同的纵坐标,
∴P(m,m+5),F(-2m,m+5),
∴d=-2m-m=-3m (-5≤m<0),
②当点P在线段EB上时(如图2),
∵P、F、G三点具有相同的纵坐标,
∴P(m,m+5),F(-2m,m+5),
∴d=m-(-2m)=3m(0<m≤5);
(3)D(0,20),G(
| 15-m |
| 2 |
| 15-m |
| 2 |
| 15+3m |
| 2 |
S△DBC=
| 1 |
| 2 |
| 1 |
| 2 |
①如图1,当S△EFC:S△DBC=2:5时,S△EFC=30,
∴S△EFC=
| 1 |
| 2 |
| 15+3m |
| 2 |
∴m=-1,
②如图2,EF交y轴于点M,当S△DME:S△DBC=2:5时,S△DME=30,
∴DM=12∴M(0,8),
可求直线EM的解析式为y=
| 2 |
| 5 |
∵
|
∴
|
∴F(-
| 10 |
| 3 |
| 20 |
| 3 |
∴m+5=
| 20 |
| 3 |
∴m=
| 5 |
| 3 |
∴当直线EF把△BCD的面积分成2:3两部分时,m的值为-1或
| 5 |
| 3 |
点评:本题考查了一次函数综合题,主要利用了待定系数法求一次函数解析式,联立两直线解析式求交点坐标,三角形的面积,难点在于要根据动点P的位置分情况讨论.

练习册系列答案
相关题目
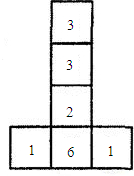 六个面上分别标有1,1,2,3,3,6六个数字的均匀立方体的表面展开图如图所示,掷这个立方体一次,记朝上一面的数为平面直角坐标系中某个点的横坐标,朝下一面的数为该点的纵坐标.按照这样的规定,每掷一次该小立方体,就得到平面内一个点的坐标.求:
六个面上分别标有1,1,2,3,3,6六个数字的均匀立方体的表面展开图如图所示,掷这个立方体一次,记朝上一面的数为平面直角坐标系中某个点的横坐标,朝下一面的数为该点的纵坐标.按照这样的规定,每掷一次该小立方体,就得到平面内一个点的坐标.求: 六个面上分别标有1,1,2,3,3,6六个数字的均匀立方体的表面展开图如图所示,掷这个立方体一次,记朝上一面的数为平面直角坐标系中某个点的横坐标,朝下一面的数为该点的纵坐标.按照这样的规定,每掷一次该小立方体,就得到平面内一个点的坐标.求:
六个面上分别标有1,1,2,3,3,6六个数字的均匀立方体的表面展开图如图所示,掷这个立方体一次,记朝上一面的数为平面直角坐标系中某个点的横坐标,朝下一面的数为该点的纵坐标.按照这样的规定,每掷一次该小立方体,就得到平面内一个点的坐标.求: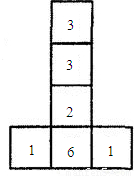 六个面上分别标有1,1,2,3,3,6六个数字的均匀立方体的表面展开图如图所示,掷这个立方体一次,记朝上一面的数为平面直角坐标系中某个点的横坐标,朝下一面的数为该点的纵坐标.按照这样的规定,每掷一次该小立方体,就得到平面内一个点的坐标.求:
六个面上分别标有1,1,2,3,3,6六个数字的均匀立方体的表面展开图如图所示,掷这个立方体一次,记朝上一面的数为平面直角坐标系中某个点的横坐标,朝下一面的数为该点的纵坐标.按照这样的规定,每掷一次该小立方体,就得到平面内一个点的坐标.求: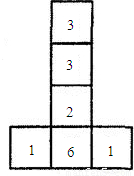 (2009•苏州模拟)六个面上分别标有1,1,2,3,3,6六个数字的均匀立方体的表面展开图如图所示,掷这个立方体一次,记朝上一面的数为平面直角坐标系中某个点的横坐标,朝下一面的数为该点的纵坐标.按照这样的规定,每掷一次该小立方体,就得到平面内一个点的坐标.求:
(2009•苏州模拟)六个面上分别标有1,1,2,3,3,6六个数字的均匀立方体的表面展开图如图所示,掷这个立方体一次,记朝上一面的数为平面直角坐标系中某个点的横坐标,朝下一面的数为该点的纵坐标.按照这样的规定,每掷一次该小立方体,就得到平面内一个点的坐标.求: